احتمال گسسته(ریاضیات) - به وبلاگ خودتون خوش آمدید

7:40 عصر شنبه 87/9/2

پیشینه‌ی نظریه‌ی احتمال، به قرن هفدهم میلادی و مطالعات بلیز پاسکال روی اعداد ظاهر شده بر تاس‌ها برمی‌گردد. پس از او لاپلاس، احتمال را به صورت نسبت پیشامدهای مطلوب به کل پیشامدها تعریف کرد. برای مثال احتمال آمدن عدد زوج، هنگام انداختن یک تاس سالم، برابر است با 3 (یعنی تعداد حالت‌هایی که ممکن است عدد زوج بیاید یا به تعبیر دیگر 2، 4 یا 6 ظاهر شود) بخش بر 6 (یعنی کل حالت‌هایی که ممکن است با انداختن تاس ظاهر شود یا به تعبیر دیگر آمدن 1، 2، 3، 4، 5 یا 6) که برابر می‌شود با ${3\over 6}$ یا ${1\over2}$ .

نظریه‌ی احتمال

چند تعریف

برای ادامه‌ی بحث، لازم است که ابتدا چند واژه را تعریف کنیم:

آزمایش تصادفی: یک آزمایش که نتیجه‌ی آن به هیچ‌وجه قابل پیش‌بینی نباشد یا اصطلاحاً تصادفی باشد؛ مثل انداختن تاس یا سکه.
فضای نمونه^[?]‌: مجموعه‌ی کل نتیجه‌هایی که ممکن است از یک آزمایش تصادفی حاصل شود؛ مثلاً در آزمایش انداختن تاس فضای نمونه به صورت ${1,2,3,4,5,6}$ است.
پیشامد^[?]: به هریک از زیرمجموعه‌های فضای نمونه‌ یک پیشامد می‌گویند؛ مثلاً ${2,4,6}$ یک پیشامد در آزمایش انداختن تاس است.
فضای نمونه‌ی هم‌شانس^[?]: در صورتی که همه‌ی اعضای فضای نمونه‌ شانس برابری برای ظاهر شدن داشته باشند یا به عبارت دیگر، شانس تمام اعضا یکسان باشد، این فضای نمونه را هم‌شانس می‌خوانیم. مثلاً آزمایش انداختن تاس سالم^[?] در فضای هم‌شانس است.

احتمال در فضای متناهی

اگر فضای نمونه‌ی ما هم‌شانس و دارای تعداد اعضای متناهی باشد، برای محاسبه‌ی احتمال وقوع یک پیشامد، فرمول لاپلاس را به کار می‌گیریم.

$p={|E|\over |S|}$

یا به عبارت دیگر، احتمال وقوع یک پیشامد برابر است با نسبت اندازه‌ی پیشامد به اندازه‌ی فضای نمونه. برای مثال اگر آزمایش انداختن تاس سالم را در نظر بگیریم که دارای فضای نمونه‌ی هم‌شانس با اندازه‌ی متناهی است، با توجه به آن‌چه پیش‌تر گفته شد، احتمال آمدن عدد 6، برابر است با اندازه پیشامد (یعنی اندازه‌ی ${6}$ که 1 است) بخش بر اندازه‌ی فضای نمونه (یعنی اندازه‌ی ${1,2,3,4,5,6}$ که 6 است). به این ترتیب احتمال آمدن عدد 6، برابر با $1\over 6$ محاسبه می‌شود.

احتمال پیشامدهای مرکب

گاهی می‌خواهیم با داشتن احتمال چند پیشامد، بتوانیم احتمال مجموعه‌ی حاصل از اعمال جبر مجموعه‌ها بر آن‌ها را نیز محاسبه کنیم. دو مورد از این موارد مهم‌تر است:

احتمال مکمل یک پیشامد: مکمل یک پیشامد زمانی اتفاق می‌افتد که خود آن پیشامد اتفاق نیفتد. به عبارت دیگر ما می‌خواهیم احتمال رخ ندادن یک پیشامد را حساب کنیم. از آن‌جا که پیشامد زیرمجموعه‌ای از فضای نمونه است، مکمل آن، مجموعه‌ی اعضای فضای نمونه‌ است که در پیشامد مورد نظر ما نیستند. به این ترتیب با توجه به فرمول لاپلاس، رابطه‌ی زیر برای محاسبه‌ی احتمال مکمل یک پیشامد، با داشتن احتمال خود آن پیشامد به دست می‌آید:

$p(\bar{E})=1-p(E)$

با توجه به آن‌چه گفته شد اثبات این رابطه بسیار ساده است.

احتمال اجتماع^[?] دو پیشامد: همان‌طور که از مفهوم اجتماع مجموعه‌ها برمی‌آید، وقوع اجتماع دو پیشامد به معنی آن است که حداقل یکی از این دو پیشامد اتفاق بیفتد. برای محاسبه‌ی احتمال اجتماع دو پیشامد، با فرض داشتن احتمال خود آن‌ها و احتمال اشتراک^[?]شان، رابطه‌ی زیر را داریم:

$p(E\cup F)=p(E)+p(F)-p(E\cap F)$

اثبات این رابطه با دانستن این‌که $|E\cup F|=|E|+|F|-|E\cap F|$ میسر است.

تخصیص احتمال

تا این‌جا بیش‌تر درباره‌ی آزمایش‌ها و فضاهای نمونه‌ای بحث کردیم که هم‌شانس هستند. با این‌همه، بسیاری از آزمایش‌ها در فضای هم‌شانس اتفاق نمی‌افتند و لذا برای محاسبه‌ی احتمال آن‌ها نمی‌توان به سادگی فرمول لاپلاس را به کار برد.

برای حل این مشکل، راه‌حل تخصیص احتمال^[?] را به این ترتیب به کار می‌بریم: به تک‌تک اعضای فضای نمونه‌ احتمالی نسبت می‌دهیم که از دو قانون زیر پیروی کند:

مقدار هر یک از این احتمال‌ها باید بین صفر و یک باشد؛ به عبارت دیگر برای هر $s\in S$ داشته باشیم:

$0\leq p(s)\leq 1$

مجموع مقدار احتمال‌های تخصیص‌داده‌شده، برابر 1 باشد؛ به عبارت دیگر داشته باشیم:

$\sum_{s\in S} p(s)=1$

به تابع احتمال p، تابع توزیع احتمال^[?] می‌گوییم.

اگر تابع احتمال به هر عضو فضای نمونه‌، مقدار یکسانی نسبت دهد، آن را توزیع یک‌نواخت^[?] می‌خوانیم.

روشن است که با توجه به آن‌چه در این‌جا تعریف کردیم، احتمال وقوع یک پیشامد برابر است با مجموع احتمال اعضایی از فضای نمونه که در آن پیشامد حضور دارند.

احتمال شرطی و استقلال پیشامدها

فرض کنید خانواده‌ای دو فرزند دارد. می‌خواهیم بدانیم اگر فرزند اول پسر باشد، با چه احتمالی فرزند دوم دختر خواهد بود؟ برای حل چنین مسئله‌ای از رابطه‌ی احتمال شرطی^[??] استفاده می‌کنیم که به شکل زیر است:

$p(E|F)={p(E\cap F)\over p(F)}$

یا به عبارت دیگر احتمال وقوع E، اگر F اتفاق افتاده باشد، برابر است با نسبت احتمال اشتراک E و F به احتمال F.

حال اگر این دو پیشامد از هم مستقل^[??] باشند، روشن است که وقوع E ارتباطی با وقوع F نخواهد داشت یا به تعبیر دیگر $p (E | F)$ همان $p (E)$ خواهد بود.

به این ترتیب می‌توانیم دو پیشامد E و F را مستقل بدانیم، در صورتی که:

$p(E\cap F)=p(E)p(F)$

توزیع احتمال دوجمله‌ای

یک آزمایش تصادفی بسیار مشهور، موسوم به آزمایش برنولی^[??]، به این شکل تعریف می‌شود:

آزمایشی تصادفی که در هر بار انجام آن تنها یا پیروزی اتفاق می‌افتد یا شکست.

با توجه به این آزمایش، در صورتی که n بار آزمایش برنولی انجام شود، و این آزمایش‌ها از هم مستقل باشند و احتمال پیروزی نیز p باشد، آن‌گاه تابع توزیع احتمال، مشهور به توزیع احتمال دوجمله‌ای^[??] خواهیم داشت که به صورت ${n\choose k}p^k(1-p)^{n-k}$ است (k تعداد پیروزی‌هاست).

علت این‌ نام‌گذاری، شباهت فوق‌العاده‌ی رابطه‌ی به‌دست‌آمده با رابطه‌ی بسط دوجمله‌ای نیوتن است.

توزیع احتمال هندسی

اگر آزمایش برنولی (که در بخش قبل معرفی شد) آن‌قدر تکرار شود تا پیروزی به دست آید، در این صورت توزیع احتمالی به دست می‌آید که به توزیع احتمال هندسی^[??] مشهور است. در این حالت فضای نمونه، تعداد اعضای نامتناهی دارد و هر عضو را می‌شود یک توالی^[??] در نظر گرفت. تابع توزیع احتمال در این حالت به شکل زیر است (p احتمال پیروزی و k تعداد دفعات لازم برای تکرار آزمایش است تا پیروزی حاصل شود):

p (1 ? p) k ? 1

توجه کنید که تعریف این توزیع را می‌توانستیم به این ترتیب انجام دهیم که آن‌قدر آزمایش تکرار شود تا نتیجه‌ی شکست به دست آید. اگر تعریف به این شکل باشد، کافی است جای p و 1-p را در رابطه‌ی به‌دست‌آمده عوض کنیم.

متغیر تصادفی، امیدریاضی و واریانس

در این بخش به معرفی سه تابع بسیار مهم مرتبط با احتمال می‌پردازیم. این تابع‌ها، کاربردهای وسیعی در نظریه‌ی احتمال و مباحث آماری دارند.

متغیر تصادفی

متغیر تصادفی^[??]، تابعی است که از فضای نمونه بر اعداد حقیقی تعریف شده است؛ یعنی هر عضو از فضای نمونه را به یک عدد حقیقی مربوط می‌کند. متغیر تصادفی را معمولاً با X نشان می‌دهند. (اشتباه نکنید! متغیر تصادفی، نه متغیر است و نه تصادفی! این تنها یک نام‌گذاری است).

مثلاً فرض کنید که خانواده‌ای دو فرزند دارد. به این ترتیب فضای نمونه‌ی حالت‌های ممکن برای این جنسیت دو فرزند به صورت {(پ،د)و(د،پ)و(د،د)و(پ،پ)} خواهد بود. حال فرض کنید متغیر تصادفی X قرار است تعداد فرزندان دختر را مشخص کند. به این ترتیب خواهیم داشت:

0=(پ،پ)X 1=(پ،د)X 1=(د،پ)X 2=(د،د)X

همان‌طور که برای یک آزمایش تصادفی، توزیع احتمال تعریف کردیم، می‌توانیم برای متغیر تصادفی نیز تابع توزیع احتمال تعریف کنیم که با (p(X=r نموده می‌شود. مثلاً در مورد همان مثال بالا، تابع توزیع احتمال به این شکل درمی‌آید:

$p(X=0)={1\over4}$ $p(X=1)={1\over2}$ $p(X=2)={1\over4}$

حال می‌توانیم دومین تابع را معرفی کنیم.

امیدریاضی

امیدریاضی^[??]، در حقیقت یک نوع میانگین‌گیری از متغیر تصادفی است. یعنی این‌که اگر یک آزمایش را بی‌نهایت‌بار تکرار کنیم و از مقدارهای متغیر تصادفی مرتبط با نتایج میانگین بگیریم، چه عددی به دست خواهد آمد. معرفی دقیق ریاضی این تابع کمک بیش‌تری خواهد کرد:

$E(X)=\sum_{s\in S} p(s)X(s)$

برای نمونه، اگر همان مثال گفته شده در بخش قبل را در نظر بگیریم، امیدریاضی تعداد دختران یک خانواده با دو فرزند به صورت زیر خواهد بود:

$0\times{1\over4}+1\times{1\over2}+2\times{1\over4}=1$

یکی از مهم‌ترین ویژگی‌های تابع امیدریاضی، خطی بودن آن است؛ یعنی اگر n متغیر تصادفی به صورت 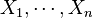$X_1,\cdots,X_n$ داشته باشیم، تساوی زیر برقرار خواهند بود:

$E(X_1+\cdots+X_n)=E(X_1)+\cdots+E(X_n)$

E (a X 1 + b) = a E (X 1) + b

برای ادامه‌ی بحث، بد نیست تعریف زیر را انجام دهیم:

دو متغیر تصادفی X و Y را مستقل می‌خوانیم در صورتی که برای هر $a,b\in \mathbb{R}$ داشته باشیم احتمال X=a و Y=b برابر است با حاصل‌ضرب احتمال X=a در احتمال Y=b.

با توجه به این تعریف، می‌توان ثابت کرد که حکم مهم زیر برقرار است:

اگر X و Y دو متغیر تصادفی مستقل باشند، آن‌گاه خواهیم داشت (E(XY)=E(X)E(Y.

اگر به یاد داشته باشید در مبحث قبل، توزیع احتمال دوجمله‌ای و هندسی را تعریف کردیم. محاسبات نشان می‌دهند که امیدریاضی توزیع احتمال دوجمله‌ای برابر $n p$ و امیدریاضی توزیع احتمال هندسی برابر $1\over p$ خواهد بود.

حال به معرفی آخرین تابع می‌پردازیم که در محاسبات آماری جایگاه ویژه‌ای دارد.

واریانس

واریانس^[??] در محاسبات آماری، یک معیار برای سنجش میزان پراکندگی داده‌ها از میانگین است. ما در این مباحث، امیدریاضی را مشابه میانگین در نظر گرفتیم و به این ترتیب واریانس را چنین تعریف می‌کنیم:

اگر X متغیر تصادفی روی فضای نمونه‌ی S باشد، واریانس X برابر خواهد بود با:

$V(X)=\sum_{s\in S} (X(s)-E(X))^2p(s)$

حکم بسیار مهمی که در محاسبات بسیار راه‌گشاست و از تعریف نتیجه می‌شود به قرار زیر است:

اگر متغیر تصادفی X روی فضای نمونه‌ی S تعریف شده باشد، واریانس از رابطه‌ی زیر نیز به دست می‌آید:

V (X) = E (X 2) ? E (X) 2

در این‌جا مقصود از $X 2$ این است که مقدارهای متغیر تصادفی را به توان 2 برسانیم.

مثلاً برای محاسبه‌ی واریانس متغیر تصادفی تعداد فرزندان دختر در یک خانواده‌ با دو فرزند (که در بخش‌های قبل توزیع احتمال و امیدریاضی آن به دست آمد)، باید به این ترتیب عمل کنیم:

${1\over4}(0-1)^2+{1\over2}(1-1)^2+{1\over4}(2-1)^2={1\over2}$

واریانس مجموع چند متغیر تصادفی مستقل را می‌توان برحسب واریانس تک‌تک این متغیرها حساب کرد:

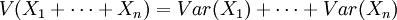
$V(X_1+\cdots+X_n)=Var(X_1)+\cdots+Var(X_n)$

تأکید می‌کنیم که این حکم فقط در صورتی قابل استفاده است که متغیرها مستقل باشند.

نظر شما ()

لیست کل یادداشت های این وبلاگ

مطالب طنز
[عناوین آرشیوشده]

[ خانه :: پارسی بلاگ :: مدیریت:: پست الکترونیک :: شناسنامه]

اوقات شرعی


	تعداد بازدید:66043
	امروز:4 دیروز :0 RSS


	درباره خودم
	امیررضا طغرلی


	لوگوی خودم



	لوگوی دوستان



	آرشیو
	تانژانت(ریاضیات) دایره مثلثاتی(ریاضیات) سینوس(ریاضیات) تابع(ریاضیات) گسل زمین شناسی گدازه آتشفشان باکتری ها جدول تناوبی عناصر1 جدول تناوبی عناصر2 عجایب هفت گانه احتمال گسسته(ریاضیات) هندسه ابوالحسن بنی صدر فرمول های مهم مثلثاتی(ریاضیات) قانون کسینوس ها(ریاضیات) فرمول اولر(ریاضیات) رادیان(ریاضیات) حل عددی معادلات دیفرانسیل معمولی(ریاضیات) جبر خطی(ریاضیات) فضای برداری(ریاضیات) دنباله(ریاضیات) تابع نمایی(ریاضیات) بهرام گور کروموزوم و میتوز عدسی ها(فیزیک) قانون کولن(فیزیک) ظرفیت گرمایی(فیزیک) قانون هوک(فیزیک) اخترشناسی1 اخترشناسی2 اخترشناسی3 اخترشناسی4 روباتیک باراک اوباما به روایت تصویر اسفند 1387


	اشتراک