امیررضا طغرلی - به وبلاگ خودتون خوش آمدید

10:20 عصر پنج شنبه 87/9/7

لنز به زبان فارسی یعنی عدسی که در واقع از ذره بینی تشکیل شده که تصویر را یر روی صفحه حساس دوربین می‌نگارد.
عدسی‌ها از ماده‌های شفاف ساخته می‌شوند و به دو نوع تقسیم می‌گردند:

همگرا
واگرا

گونه‌های عدسی

عدسی همگرا: در عدسی همگرا، پرتوهای تابش، پس از شکست و گذر از عدسی، به هم نزدیک می‌شوند (یعنی همگرا می‌شوند). در عدسی‌های همگرا، لبه‌ها نازکتر از وسط آن است و به طور معمول برای کاربردهای متفاوت به شکل‌های دو کوژ، کوژتخت و هلالی همگرا ساخته می‌شوند.

عدسی واگرا: در عدسی‌های واگرا، پرتوهای تابش، پس از شکست و گذر از عدسی، از هم دور می‌شوند (یعنی واگرا می‌شوند). لبه? این عدسی‌ها پهن‌تر از وسط آن است و به شکل‌های دو کاو، کاو تخت و هلالی واگرا ساخته می‌شوند.

عدسی‌های مرکب

عدسی‌های گوناگون بر پایه? ساختار

عدسی‌ها را بر پایه? ساختار اینگونه بخش‌بندی می‌کنند:

عدسی کوژ - تخت: آنچنان عدسی است که یک طرف آن کوژ و یک طرف آن تخت می‌باشد.
عدسی دو کوژ: آنچنان عدسی است که هر دو طرف آن کوژ می‌باشد.
عدسی هلالی (کوژ): آنچنان عدسی است که یک طرف آن کوژ و طرف دیگرش کاو باشد.
عدسی تخت - کاو: آنچنان عدسی است که یک طرف آن کاو و طرف دیگرش تخت باشد.
عدسی دو کاو: آنچنان عدسی است که هر دو طرف آن کاو باشد.
عدسی هلالی (کاو): آنچنان عدسی است که یک طرف آن کوژ و طرف دیگرش کاو باشد.

دستگاه‌های نوری دارای عدسی

بیش‌تر دستگاههای نوری شامل دو گونه عدسی می‌باشند که یکی را که نور، نخست بر آن می‌تابد و در ورودی دستگاه کار گذاشته می‌شود عدسی شیئی و دومی را که در خروجی دستگاه قرار دارد و نور از آن خارج می‌شود عدسی چشمی گویند. از جمله از این دستگاهها میکروسکوپ نوری، زیر دریایی، میکروسکوپ پلاریزان، دوربین‌های دو چشمی، دوربینها، انواع عینکها و... را می‌توان نام برد.

عدسی چشم

عدسی چشم، یک عدسی همگرای دوکوژ است که از ماده‌ای ژله مانند، انعطاف‌پذیر و شفاف ساخته شده‌است.
ضریب شکست عدسی چشم تقریباً ???/? است.^{[نیازمند منبع]}

فرمول عدسی ها

این فرمول ها برای محاسبه ی فواصل مختلف بکار برده می شوند:

1: نسبت یک به روی q بعلاوه نسبت یک به روی q مساوی است با نسبت یک به روی F که در اینجا P فاصله شئ تا عدسی و q فاصله تصویر تا عدسی است و F فاصله ی کانونی است در عدسی های کوژ یا محدب چون تصویر مجازی است علامت آن منفی و بقیه موارد به جز یک مورد عدسی کاو یا مقعر مثبت است.

2: $F = r / 2$ یا بر عکس آن $r = 2 * F$ توجه کنید r شعاع عدسی است.

3: فرمول بزرگنمایی خطی آینه m برابر است با نسبت "A"B به AB و مساوی است با q به روی p M = بزرگنمایی خطی (میزان چند برابر شدن تصویر) AB = طول شئ و "A"B = طول تصویر

توجه: در همه ی فرمولها همه ی واحد با باید از یک نوع باشند مثلآ همه ی موارد بر حسب سانتی متر باشند

نظر شما ()

10:11 عصر پنج شنبه 87/9/7

میتوز و کروموزوم

نویسنده: امیررضا طغرلی

میتوز (به انگلیسی: Mitosis) از مراحل چرخه سلولی است.

میتوز تکثیر سلول به دو سلول نوزاد با کروموزومهای مشابه میباشد.^[?]

میتوز خود به چند مرحله بترتیب تقسیم میگردد:

قسمت زرد رنگ این چرخه سلولی مراحل میتوز را نشان میدهد.

کرو موزوم

به زبان ساده می‌توان کروموزوم‌ها را به بسته‌های مواد ژنتیکی تشبیه کرد که درون هسته‌ی سلول‌ها ذخیره شده‌اند. و در واقع به شکل مولکول‌های دی‌ان‌ای همراه با پروتئین‌ها هستند که به این بسته‌هارنگین‌تن‌ یا کروموزوم گفته می‌شود.

پروتئین اصلی که در یوکاریوت‌ها مسئول بسته‌بندی دی‌ان‌ای است هیستون نام دارد. سلول‌های یوکریوتی تعداد مشخصی کروموزوم دارند. مثلاً سلول‌های انسان دارای ?? جفت کرووموزوم می‌باشد. سلول‌های انسان به جز تخمک و اسپرم به صورت دیپلوئید می‌باشند یعنی دارای ? سری از کروموزوم‌های همانند می‌باشند. سلول‌های تخمک و اسپرم‌ها پلوئید هستند یعنی دارای یک سری از هر کروموزوم‌ند. سلول‌های پروکاریوتی (باکتری‌ها) معمولاً دارای یک کروموزوم می‌باشند. البته باکتری‌هایی هم هستند که دارای چند کروموزوم می‌باشند اما این باکتری‌ها نادر هستند. کروموزوم باکتری‌ها به صورت حلقوی است. باکتری‌ها (و برخی مخمرها) علاوه بر کروموزوم اصلی دارای یک یا چند پلاسمید نیز می‌باشند. انسان‌ سالم‌ دارای‌ ?? جفت‌ رنگین‌تن است‌. ?? جفت‌ رنگین‌تن که‌ تعیین‌‌کننده‌ منش های‌ ارثی‌ به‌ غیر از جنس‌ (نر و ماده‌) است‌ و خودتن (اتوزوم‌) نامیده‌ می‌شود. یک‌ جفت‌ دیگر را رنگین‌تن‌ جنسی‌ می‌گویند. رنگین‌تن‌های جنسی‌ در مردان‌ طبیعی به‌ صورت‌ XY و در زنان طبیعی‌ XX است.

نظر شما ()

9:55 عصر پنج شنبه 87/9/7

مقاله

نویسنده: امیررضا طغرلی

رشته مهندسی رباتیک در ایران

رشته فنی مهندسی رباتیک یکی از رشته های میان رشته ای جدید در ایران میباشد ،جدید بودنش میتواند بدلیل تاسیس در حد اکثر 15 سال گذشته باشد و میان رشته ای است به دلیل اشتراکاتی که با رشته های مهندسی برق گرایشات الکترونیک و کنترل و همچنین مهندسی مکانیک گرایش طراحی جامدات و مهندسی کامپیوتر گرایش نرم افزاردارد.

گاهی اوقات حتی افراد تحصیل کرده نیز به اشتباه ،گمان میبرند مهندس رباتیک ،مهندس برق نیز می باشد علاوه بر این مکانیک و کامپوتر نیز هست،در صورتی که برای دانشجوبان رباتیک واضح بودن این اشتباه غیر قابل انکار است که بقیه رشته ها یک مهندس رباتیک تنها یک مهندس رباتیک است. چرا که به صرف ارائه دروسی چون مداراهای الکترونیکی و منطقی و ریز پردازنده در برنامه درسی مهندسی کامپیوتر-نرم افزار و اشتراک این دروس در رباتیک و مهندسی الکترونیک ،نمیتوان نسبتی از الکترونیک و رباتیک به کامپیوتر داد.وظیفه و کربرد ها متفاوت است.شاید یکی از نمونه های فریبنده آگهی های استخدام کار شرکتها یا کارخانه ها باشد که آنهم بدلیل کاربرد مورد انتظار آنها،نام چند رشته مهندسی را در کنار یکدیگر قرار میدهند.

به عبارتی این دیگر بستگی به نیاز صنعت و کارخانه ها دارد که بسته به نیازشان ، رشته های دانشگاه تاسیس شده اند، رشته رباتیک نیز از این اصل مستثنا نیست .

یک مهندس رباتیک حتی با وجود توانایی در برخی از موارد اختصاصی موجود در دیگر رشته ها،تنها یک مهندس رباتیک است این اصل را میتوان برای دیگر رشته های فنی مهندسی تعمیم داد.

رشته های جدید برای نیاز های جدید و پاسخ به آنها طراحی شده اند وبه طبع آن توانایی افراد تحصیل کرده نیز بهترین پاسخ برای این نیازها میباشد که رشته رباتیک نیز پاسخگو به نیاز رباتیکی صنعت میباشد.

این رشته را می توان یکی از گرایشهای مکاترونیک محسوب کرد. در ایران دانشگاه شاهرود در مقطع کارشناسی رشته روباتیک دارد.

ارتباط با دیگر رشته‌ها

در حقیقت اگر یک مهندس رباتیک قصد نو آوری و ایجاد یک تکنولوژی را در سر بپروراند و برای مثال طرح یک ربات فوتبالسیت آدم واره را بریزد ملزوم به استفاده از دروسی که قبلا ً ،فراگرفته و یا تکمیل آنها میباشد به عبارتی باید در برنامه نویسی و تنظیم الگوریتم بهینه ،طراحی مدارهای الکتریکی و الکترونیکی مورد نیاز، طراحی مکانیزم عالی و ی نقص و کار امد در ایجاد تعادل پویا مهارت کافی داشته باشد.

به خصوص در زمینه طراحی کامیپوتری مدارها ، اجزاء و از همه مهمتر برنامه نویسی در سطح بالای قرار داشته باشد تا این نیازها را برطرف کند.

بر فرض برای طراحی یک ربات آی کاوشگر باید با روشهای عایق بندی آشنا باشد و یا در یک ربات پرنده با طراحی سیستم آئرودینامیکی تا حدودی آشنایی داشته باشدو یا در تولید و ساخت ربات جنگنده، آشنا به موارد مختلف و ویژگی های مختلف آنها مثل استحکام و سبک وزنی یا انعطاف و سختی و دیگر مورد این چنینی باشد.

البته مثل دیگر رشته های میان رشته ای ارتباط های زیادی میتوان با دیگر علوم و فنون پیدا کرد که موارد فوق مربوط به رباتیک بودند که این ارتباطات در این رشته بیشتر از دیگر رشته هاست.

صنعت رباتیک

امروزه استفاده از رباتها واتوماسیون غیر قابل انکار و معرفی شده برای تمام صنایع و کارخانه ها میباشد به طوری که کارخانه ها روز به روز به این سمت روی می آورند دلیلش هم مشخص است زیرا بازده ای بهتر و سرعت دقت کم هزینه بودن دیگر خصوصیات مورد انتظار را به ارمغان میآورد.

رباتها اولین بار در سال 1954 در صنعت به کارگرفته شدند که یک بازوی ربات یا Manipulator نام داشت که تنها 3 درجه آزادی بود.رباتهای صنعتی امروزی اکثراً همان بازوی رباتیکی هستند ولی با 6 درجه آزادی و خیلی پیشرفته تر نبست به گذشته کار میکنند رباتها در صنعت به شیوه ها و روشها و مدلهای مختلفی به کارگرفته میشوند.

گستردگی علم رباتیک

همان طور که در ارتباط این رشته با دیگر رشته ها ذکر شد برای فعالیت و نوآوری و تحقیق و پیشرفت به جرات میتوان گفت یکی از وسیع ترین شاخه های فنی مهندسی،رشته مهندسی رباتیک میباشد. برای مثال رباتی را معرفی میکنم که ارتباط بسیار کمی با رشته های فنی مهندسی و علوم پایه دارد،ربات جراح تحت فرمان پزشک جراح در اتاق عمل با حضور مستقیم پزشک و یا غیر مستقیم و با کمک اینترنت ،نمودی از پیشرفت این رشته است که بسیار مفید و حیاتی میباشد.تصور کنید رباتی را که شما طراحی کرده اید وسیله ای برای نجات یک بیمار و بهبودی وی شده است که قطعاَ لذت موفقیت آن خستگی زحمتتان را از بین میبرد.

نمونه ی بارز دیگر گستردگی علم رباتیک، که بسیار مورد توجه کشورهای مختلف مثل ژاپن،کره،آمریکا و ایران و چند کشور دیگر میباشد،رباتهای امداد و نجات هستنند که یاری رسان گروه امداد در حوادث غیر قابل پیش بینی میباشد.به هر حال این گرایش از رباتیک آن قدر اهمیت داشته است که مسابقاتی تحت عنوان شبیه سازی امداد و نجات در روبوکاپ برگزار میگردد.

وظیفه اصلی رباتهای امداد رسان پیدا کردن مصدومین و اعلام مکان آنها به سرور میباشد.

رباتها در پروژه های JPL شرکت فضایی NASA نقش مهمی دارند از جمله آنها Spriteو Sojourner می باشد.این نیز استفاده دیگری از رباتیک میباشد .

مصارف رباتها در همه ابعاد زندگی انسان به سرعت در حال گسترش است تا کارهای سخت و خطرناک را به جای انسان انجام دهند مثل بررسی وضعیت داخلی راکتورها هسته ای که یک ربات هیچ گاه تحت تاثیر تشعشعات رادیو اکتیو قرار نمیگیرد و این یک جایگزینی خوب و مفید رباتها میباشد.

نیاز کارخانه ها و صنایع جهان و آینده شغلی

کارخانه های دارای ربات های صنعتی وخطوط اتوماسیون و به خصوص بازوهای رباتیک اولین کارخانه ها در جذب نیروی پرسنلی در این رشته اند و در اولویت اول این کارخانه ها مربوط به صنایع ماشین سازی و سپس شرکت های تولید کننده تراشه های سیلیکونی والکترونیکی میباشند ،از جمله این کارخانه ها در ایران که دارای خطوط اتوماسیون و یا بازوهای رباتی و یا دیگر رباتهای صنعتی هستند، میتوان نام برد به شرح زیر است: کارخانه ماشین سازی ایران خودرو،ماشین سازی سایپا،کاشی سمنان،کاشی یزد،تراکتور سازی تبریز،کیش خودرو،رب تبرک،کنستانتره شاهرود و چندین کارخانه دیگر که اکثرا ماشین سازی هستنند را میتوان نام برد.

رباتیک و ربات در ایران

در زمینه تولید ربات هنوز کسی در ایران چیزی نشنیده است، مگر تعمیر و بازسازی رباتهای وارداتی تنها بخش ،ساخت ربات ،برای مسابقات رباتیک میماند که تیم های ایرانی کم ترین حضور را دارند آنهم بدلیل هزینه قابل توجه ساخت میباشد که نبود حمایت دانشگاه ها چه مالی و چه هر چیز دیگری ،نبود پشتیبان تبلیغاتی که البته این مورد در حال حاضر به جرات میتوان گفت یکی از قویترین کشورها در مسابقات روبوکاپ در بخش شبیه سازی امداد و نجات و شبیه سازی فوتبال ،ایران میباشد.شاید علت امتناع فعالان رباتیک در بخش های دیگر کم هزینه بودن این رشته باشد و متاسفانه علت آن در اکثر مواقع پولی است.جالب است بدانید در مسابقات برمن آلمان که 24 خرداد برگزار شد اکثر تیم های شرکت کننده در بخش شبیه سازی رباتهای امداد و نجات ایرانی بودند. در مورد ایران البته با توجه به تمام مطالب بیان شده در مورد ایران جای امید واری است که اکثر کارخانه ها و صاحبان صنایع بر اساس دلایل مختلف مثل رقابت روز به روز به سمت استفاده از ربات روی آورده اند و این موضوع دلیلی بر وجود و حتی رشد بسیار چشم گیر بازار شغلی این رشته دارد.

چشم انداری از رباتیک

شهری را تصور کنید که رباتها در اکثر فعالیت های انسانی و بشری کمک رسان بشر شده اند.به یقین که نگاهی با کمی دورنگری و کمی بزرگ نمایی از آینده این رشته بسیار نگران کننده و شاید خطرناک باشد.تصور این که رباتی شما را در یک معمله بفریبد و یا رباتی که دارای احساس و اندیشه و جماعاتی رباتی که بر سر مسایل مورد نظر شان مثل کم توجهی به آنها شروع به شورش کنند و دیگر موارد که اکنون خنده دار و در باطن نگران کننده است.البته مفید بودن ساخته دست بشر در درجه اول قرار میگیرد.

نظر شما ()

8:20 عصر چهارشنبه 87/9/6

دنباله

نویسنده: امیررضا طغرلی

در ریاضیات دنباله تابعی است با دامنه اعداد طبیعی. این توابع کاربردهای فراوانی در حساب دیفرانسیل و انتگرال و سایر شاخه های ریاضیات دارند و گاهی نیز به فراخور نیاز نام آنها تغییر می یابد. به عنوان مثال در نظریه تحلیلی اعداد به دنباله ها تابع حسابی می گویند

مفهوم دنباله

مجموعه اعداد زوج طبیعی را در نظر بگیرید:

$\mathbb{N}_e=\{2,4,6,8,...,2n,...\}$

اولین عضو این مجموعه عدد 2 است و n امین عضو آن 2n است.

حال مجموعه اعداد طبیعی را در نظر بگیرید:

$\mathbb{N}=\{1,2,3,4,5,...,n,...\}$

با کمی دقت متوجه می‌شویم که می‌توان یک تابع از مجموعه اعداد طبیعی به مجموعه اعداد طبیعی زوج تعریف نمود که هر عضو از مجموعه اعداد طبیعی را به یک عضو از مجموعه اعداد طبیعی زوج متناظر کند.

به عبارت دقیقتر می توان تابع $f:\mathbb{N}\to \mathbb{N}_e$ را با ضابطه $\forall n\in \mathbb{N}:f(n)=2n$ تعریف کرد.اگر این تناظر را به صورت مجموعه زوج های مرتب بنویسیم خواهیم داشت:

f = {(1,2),(2,4),(3,6),(4,8),...,(n,2 n),...}

متوجه می‌شویم تابع f از مجموعه اعداد طبیعی به مجموعه اعداد طبیعی زوج، و هر عضو از دامنه خود را دو برابر می‌کند و به یک عضو از مجموعه اعداد طبیعی زوج متناظر می‌کند.

حال در مثالی دیگر تابع $g (x) = (x ? 3) 2 + 1$ را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم:

g (1) = 5, g (2) = 2, g (3) = 1, g (4) = 2,...

مشاهده می‌کنید این تابع نیز هر عدد طبیعی را به عنوان متغیر دریافت می‌کند و آن را به یک عدد دیگر نسبت می‌دهد.

نمونه های دیگری نیز از این توابع وجود دارد مثلاً توابع f(n)=n² یا $f(n)=\sqrt{n}$ ، که در آنها n عددی طبیعی است.

به چنین توابعی که از از مجموعه اعداد طبیعی به یک مجموعه دیگر تعریف می‌شوند دنباله می‌گوییم.

در دنباله اعداد طبیعی زوج، عدد 2 از برد تابع را جمله اول، عدد 4 را جمله دوم و به همین ترتیب عدد 2n را جمله n ام دنباله می‌گوییم. همین شیوه برای سایر دنباله‌ها نیز اعمال می‌شود.

به عبارت دقیق تر اگر (f(n ضابطه یک دنباله باشد جمله k ام این دنباله را (f(k تعریف می کنیم.

در یک دنباله، اعداد طبیعی در دامنه به گونه‌ای به اعضای برد متناظر می‌شوند که عدد طبیعی متناظر شده بیانگر شماره آن جمله در برد باشد.

به عنوان مثال در دنباله اعداد طبیعی زوج، عدد 1 در دامنه به عدد 2در برد که اولین جمله دنباله است متناظر می‌شود و عدد 10 از دامنه به عدد 20 از برد که جمله دهم است متناظر می‌شود و به همین ترتیب عدد n‌ در دامنه به عدد 2n از برد که جمله n ام است متناظر می شود.

تعریف دنباله

دنباله (sequence) تابعی است که دامنه آن مجموعه اعداد طبیعی یا قطعه ای از مجموعه اعداد طبیعی باشد. پس در حالت کلی یک دنباله چون f تابعی است از مجموعه اعداد طبیعی به توی یک مجموعه ای دیگر چون A.

$f:\mathbb{N}\to A$

اگر دامنه دنباله قطعه ای از مجموعه اعداد طبیعی باشد دنباله را متناهی می‌گوییم و اگر دامنه دنباله خود مجموعه اعداد طبیعی یا زیرمجموعه ای نامتناهی از آن باشد، دنباله را نامتناهی می‌گوییم.

به عنوان مثال دنباله اعداد طبیعی زوج کوچک‌تر از 10 یک دنباله متناهی است چرا که دامنه آن قطعه ای از مجموعه اعداد طبیعی یعنی

$\mathbb{N}_5=\{1,2,3,4,5\}$

است و دنباله اعداد زوج دنباله‌ای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است.

برای مشخص کردن یک دنباله مانند هر تابع دیگر، باید دامنه و ضابطه آن را مشخص کرد. ضابطه یک دنباله را در اصطلاح جمله عمومی آن دنباله می‌گوییم. اگر f یک دنباله باشد جمله عمومی آن را با {(f(n} و یا به صورتی معمول‌تر به صورت {f_n} نشان می‌دهیم.

به عنوان مثال دنباله اعداد طبیعی زوج را به این صورت

{f n} = {2 n}

نشان می دهیم. همچنین برای نمایش مقدار دنباله f به ازای عدد طبیعی از نماد (f(n و یا معمولاً از نماد f_n استفاده می‌کنیم.

به عنوان مثال در دنباله اعداد طبیعی زوج داریم:

f 1 = 2, f 2 = 4,..., f n = 2 n

دنباله حقیقی

دنباله {f_n} را دنباله حقیقی می‌گویند هرگاه تابعی از مجموعه اعداد طبیعی به مجموعه اعداد حقیقی باشد.

به عنوان مثال دنباله

$\{a_n\}=\{\frac{n+3}{2n-1}\}$

دنباله‌ای حقیقی است چرا که برد آن از مجموعه اعداد حقیقی است.

لازم به توضیح است معمولاً منظور از دنباله، دنباله ای حقیقی است.

نمودار یک دنباله

از آنجا که دنباله یک تابع با دامنه عداد طبیعی است می‌توان دنباله را به‌وسیله نمودار نیز نمایش داد. این نمایش با دو روش انجام می‌شود. در یک روش می‌توان مانند توابع دیگر آن را در دستگاه مختصات دکارتی رسم کرد و در روشی دیگر می‌توان جملات آن را به همراه ذکر شماره آن جمله روی محور اعداد نشان داد. با ذکر یک مثال دو روش را توضیح می‌دهیم.

به عنوان مثال می‌خواهیم دنباله اعداد زوج را به هر دو روش نشان دهیم:

به‌وسیله رسم نمودار در دستگاه مختصات دکارتی: برای این منظور محور افقی را برای متغیر انتخاب کرده و محور عمودی را برای نمایش تغییرات جملات دنباله استفاده می‌کنیم.

به‌وسیله رسم نمودار روی محور اعداد: برای این منظور روی محور اعداد مقدار جملات دنباله را یافته و شماره جمله را در بالا آن می‌نویسیم.

جمله عمومی یک دنباله

همانطور که گفته شد یک دنباله تابعی با دامنه مجموعه اعداد طبیعی است پس برای دنباله ها در حالت کلی می‌توان ضابطه تعیین کرد که به ضابطه یک دنباله جمله عمومی آن دنباله می‌گویند.

جمله عمومی یک دنباله به منزله یک قانون است که به‌وسیله آن هر عضو از دامنه(مجموعه اعداد طبیعی) به یک عضو از مجموعه برد متناظر می‌شود و به ازای هر مقدار از متغیر n، جملات دنباله را تولید می‌کند.

به عنوان مثال جمله عمومی دنباله اعداد طبیعی زوج به صورت {2n} است که همانند ضابطه تابع به‌وسیله آن می‌توان با قرار دادن هر n طبیعی جمله n ام دنباله را بدست آورد.

البته لازم به ذکر است جمله عمومی همه دنباله ها را نمی توان تعیین کرد.

به عنوان مثال تا کنون جمله عمومی برای دنباله اعداد اول تعیین نشده است. همچنین ممکن است یک سری از اعداد را به عنوان جملات دنباله انتخاب نمود که نتوان میان آنها رابطه ای برقرار نمود و جمله عمومی برای آنها نوشت. حال ممکن است این سوال پیش بیاید که آیا با در اختیار داشتن جملات یک دنباله می توان جمله عمومی آن را تعیین کرد؟

پاسخ را با یک مثال بررسی می‌کنیم. دنباله زیر را در نظر بگیرید:

{t n} = {3,5,7,...}

می‌خواهیم جمله عمومی این دنباله را با توجه به جملاتش تعیین کنیم. با مشاهده‌ی جملات ممکن است حدس شما این باشد که این دنباله، دنباله اعداد طبیعی فرد بزرگ‌تر از یک است و جمله عمومی آن را می‌توان به این صورت نوشت:

{t n} = {2 n + 1}

اما این ممکن است یک جمله عمومی برای این دنباله باشد. ممکن است جملات دنباله در ادامه به این روال پیش نروند و جمله چهارم این دنباله عددی چون 9 نباشد!

چرا که ما از جمله سوم به بعد دنباله هیچ اطلاعی نداریم و هر عدد دیگری نیز می‌تواند باشد!

به عنوان مثال جمله عمومی دنباله فوق را می‌توان به این صورت نوشت:

{a n} = {(n ? 1)(n ? 2)(n ? 3) + 2 n + 1}

با نوشتن جملات این دنباله داریم:

{a n} = {3,5,7,15,...}

مشاهده می‌کنید جملات این دنباله تا جمله سوم همانند دنباله {t_n} است ولی از جمله سوم به بعد مانند آن دنباله عمل نمی کند.

پس همواره از روی جملات یک دنباله نمی‌توان جمله عمومی آن را به درستی تعیین کرد. اما معمولاً برای نوشتن جمله عمومی یک دنباله با توجه به جملات آن، ساده ترین حالت را در نظر می‌گیریم. لذا جمله عمومی

{t n} = {2 n + 1}

برای این دنباله و زودتر به ذهن خطور می‌کند.

رابطه بازگشتی و دنباله بازگشتی

به دنباله اعداد زوج دقت کنید: ...,2,4,6,8,10,12

با کمی دقت در می‌یابید که برای بدست آوردن هر جمله کافی است جمله قبل را با عدد دو جمع کنید. به عنوان مثال برای بدست آوردن جمله پنجم(10) کافی است جمله چهارم(8) را با عدد دو جمع کنید. به این رابطه که بین جملات این دنباله برقرار است رابطه بازگشتی می گوییم.

تعریف: در بسیاری از دنباله‌ها بین هر جمله و جملات ماقبل یک رابطه‌ای وجود دارد که به‌وسیله آن می‌توان جملات بعدی را تعیین نمود. به چنین رابطه‌ای، رابطه بازگشتی می‌گوییم و به دنباله‌هایی با این رابطه، دنباله بازگشتی می‌گوییم.

از معروف ترین این دنباله ها می توان به دنباله فیبوناتچی و دنباله لوکا اشاره کرد.

به عنوان مثال دنباله فیبوناتچی دارای چنین رابطه‌ای است که به‌وسیله آن مشخص می‌شود:

$F_1=F_2=1,\forall n onload=$ 2: F_n=F_{n-1}+F_{n-2}" src="http://upload.wikimedia.org/math/e/d/7/ed794d0f654945713be1153997154a76.png">

که جملات آن به این صورت است: ...,1,1,2,3,5,8,13,21

مشاهده می‌شود برای بدست آوردن هر جمله از جمله دوم به بعد کافی است دو جمله ماقبل آن جمله را با هم جمع کنیم. مثلاً برای محاسبه جمله نهم داریم:

F 9 = F 8 + F 7 = 21 + 13 = 34

یکنوایی دنباله‌ها

دنباله {a_n} را:

صعودی (نا نزولی) می‌گوییم هرگاه

$a_1\le a_2\le a_3\le ...$

یا به عبارت دیگر برای هر عدد طبیعی n داشته باشیم

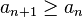
$a_{n+1}\ge a_n$

همچنین اگر جملات دنباله همگی مثبت باشند صعودی بودن دنباله را می‌توان با شرط زیر بیان کرد:

$\frac{a_{n+1}}{a_n}\ge 1$

نزولی(ناصعودی) گوییم هرگاه

$a_1\ge a_2\ge a_3\ge ...$

یا به عبارت دیگر برای هر عدد طبیعی n داشته باشیم

$a_{n+1}\le a_n$

همچنین اگر جملات دنباله همگی مثبت باشند نزولی بودن دنباله را می‌توان به صورت زیر بیان کرد:

$\frac{a_{n+1}}{a_n}\le 1$

دنباله صعودی یا نزولی را یکنوا می‌گوییم.

همچنین دنباله {a_n} را اکیداً صعودی می‌گوییم هرگاه برای هر عدد طبیعی n داشته باشیم

a n + 1 > a n

و دنباله را اکیداً نزولی می‌گوییم هرگاه

a n + 1 < a n

یک دنباله را اکیداً یکنوا می‌گوییم هرگاه اکیداً صعودی یا نزولی باشد.

حد دنباله

از آنجا که دنباله نیز تابع می‌باشد می‌توان حد آن را نیز بررسی کرد که برای اطلاع از نحوه تعریف حد دنباله‌ها و محاسبه آنها می‌توانید به مقاله حد دنباله رجوع کنید.

نظر شما ()

8:16 عصر چهارشنبه 87/9/6

تابع نمایی

نویسنده: امیررضا طغرلی

تابع نمایی تابعی در ریاضیات است. معمولا این تابع به صورت ‎ $exp(x)$ ‎ یا برابر آن $e x$ نوشته می‌شود. که $e$ عددی ثابت برابر عدد اویلر یا به طور تقریبی برابر ??????????? می‌باشد. البته می‌توان این تابع را به صورت $a x$ نیز تعریف کرد، استفاده از الگوریتم نشان می‌دهد که:

$\,\!\, a^x=(e^{\ln a})^x=e^{x \ln a}$

این تابع را تابع نمایی با پایه a می‌خوانیم که a نیز عددی ثابت است. در بسیاری علوم وقتی از تابع نمایی صحبت می‌شود منظور تابع $k a x$ می‌باشد، که a را پایه می‌نامند. در این صورت a عددی ثابت و مثبت است.

عموماً متغیر $x$ می‌تواند هر عدد حقیقی یا مختلط باشد و یا حتی می‌تواند شئ ریاضی کاملاً متفاوتی اختیار کند

نظر شما ()

8:13 عصر چهارشنبه 87/9/6

فضای برداری

نویسنده: امیررضا طغرلی

در ریاضیات، فضای برداری یا فضای خطی به مجموعه‌ای از اشیاء ریاضی (به نام بردار‌ها) گفته می‌شود که در مورد آن‌ها دو عمل جمع برداری و ضرب نرده‌ای به نحوی تعریف شده باشد که اصول موضوع چندی اقناع شود.

از جمله? معمول‌ترین فضاهای برداری در ریاضیات، و کاربردهای آن، فضاهای برداری حقیقی و فضاهای برداری مختلط هستند، که به ترتیب بر روی میدان‌های اعداد مختلط و اعداد حقیقی تعریف می‌شوند.

فضای برداری مجموعه‌ای از بردارهاست که مقیاس‌پذیرند و قابلیت جمع شدن را دارند

تعریف

یک فضای برداری یا فضای خطی از موارد زیر تشکیل شده است:^[?]

میدان $F$ متشکل از کمیت‌های نرده‌ای
مجموعه $V$ از اشیاء با نام بردار
عمل جمع با این تعریف که برای هر ? و ? در V، ? + ? در V با این شرایط:
- $\alpha + \beta = \beta + \alpha \,$
- $? + (? + ?) = (? + ?) + ?$
- بردار یکتای $0$ وجود دارد به طوریکه به ازای هر $?$ عضو $V$ ، $? + 0 = ?$
- به ازای هر بردار $?$ عضو $V$ ، بردار یکتای $? ?$ وجود دارد به طوریکه $? + ( ? ?) = 0$
عمل ضرب با این تعریف برای هر بردار ? در V و اسکالر c در میدان F، با این شرایط:
- به ازای هر $?$ در $V$ ، $1? = ?$
- $(c 1 c 2)? = c 1 (c 2 ?)$
- $c (? + ?) = c ? + c ?$
- ‎ $(c 1 + c 2)? = c 1 ? + c 2 ?$

نظر شما ()

8:11 عصر چهارشنبه 87/9/6

جبر خطی

نویسنده: امیررضا طغرلی

کاربردها

جبر خطّی و کارائی‌های فراوان و گوناگون آن در ریاضیات و محاسبات گسسته طیف گسترده و وسیعی را شامل می گردد. علاوه بر کاربردهای آن در زمینه‌هایی از خود ریاضیات همانند جبر مجرد، آنالیز تابعی، هندس? تحلیلی، و آنالیز عددی، جبر خطّی استفاده‌های وسیعی نیز در فیزیک، مهندسی، علوم طبیعی، و علوم اجتماعی پیدا‌کرده است.

مقدمه

آغاز نمودن مبحثی با اهمیت و همه‌جاگیری جبر خطی یکی از دشوار‌ترین کارهاست، چرا که، با جهت‌گیری‌ها، تعبیرات، تعمیمات، و آینده‌بینی‌های زیادی روبرو می‌شویم. شاید یکی از انتخاب‌های مناسب این گونه باشد:

ماتریس و بردار زیر را در نظر می‌گیریم:

$M = \begin{bmatrix} 1 & 2 \\ 2 & 1 \\ \end{bmatrix}, v = \begin{bmatrix} 2 \\ 1 \\ \end{bmatrix}$

با ضرب ماتریس و بردار داریم:

$M v = \begin{bmatrix} 1 & 2 \\ 2 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 4 \\ 5 \\ \end{bmatrix} = w$

نتیجه? فوق را می‌توان در تراز‌های معنائی گوناگونی مورد دقت و بررسی قرار داد. برخی از ملاحظات این گونه است:

ماتریس $M$ به عنوان عمل‌گری بر روی بردار $v$ عمل نموده و آنرا به بردار $w$ تبدیل کرده است. $M$ می‌تواند ثابت انگاشته شده و دستگاهی ساده را نمایندگی کند، که در آن صورت، بردار $v$ اطلاعات یا داده‌هایی را می‌نمایاند که به نوعی به سیستم داده شده است.

سیستم $M$ درست مثل پردازش‌گری اطلاعات را به دانش تبدیل می‌کند. شاید یکی از روشن‌ترین مثال‌های کوتاه برای مفهوم فرایند تبدیل اطلاعات به دانش همین باشد.

مقادیر خاص

مقادیر خاص و بردارهای خاص از جمله? پرکاربردترین و جوهری‌ترین مؤلفه‌های ماتریس‌ها و عمل‌گر‌های خطی می‌باشد. مفهوم و عملکرد این اشیاء ریاضی را باید از جنس تلخیص، فشرده‌سازی اطلاعات، و ساده و آسان حل کردن مسائل خطی دشوار دانست.

فضاهای برداری

از آن‌جا که بسیاری از کمیت‌های فیزیکی مثل نیرو، سرعت، و شتاب هم اندازه (بزرگی) دارند و هم راستا، آن‌ها را بردار نامیده‌اند.

نظر شما ()

8:5 عصر چهارشنبه 87/9/6

حل عددی معادلات دیفرانسیل معمولی

نویسنده: امیررضا طغرلی

معمولاً بسیار سخت است که یک روش حل تحلیلی برای بسیاری از معادلات دیفرانسیل پیدا کنیم. این مساله ممکن است به این خاطر باشد که، معادلات غیر خطی هستند یا اینکه دارای ضریبی هستند که با زمان تغییر می‌کند. برای مثال در معادلات دیفرانسیل خطی ضریب‌دار، هرچه مرتبه بیشتر باشد حل آن سخت‌تر می‌شود. یا بخاطر اینکه ورودی‌های زیادی دارد در شرایط مختلف مشکل تر است. روش‌های زیادی وجود دارد که جواب معادلات دیفرانسیل را تقریب می‌زند. این روش‌ها، نام‌های گوناگونی دارند : روش‌های عددی، انتگرال عددی یا راه حل‌های تقریبی.

تمام روش‌هایی که در اینجا بیان شده راه حل دقیق را ایجاد نمی‌کند و فقط یک تقریب به‌دست می‌آید. چون این روش‌ها دارای محاسبات زیادی هسند، تنها جواب‌هایی در فواصل زمانی مجزا می‌دهند. مشخصا جواب‌ها در زمان ابتدایی شرایط وفاصله زمان‌های مشخص، h، بدست می‌آید. (i.e., at t=to, to+h, to+?.h,... , to+k.h).

این پیچیدگی ادامه دارد زیرا، این روش‌ها فقط برای حل معادلات دیفرانسیل مرتبه اول معتبر هستند. به هرحال محدودیت جدی برای معادله مرتبه nام وجود ندارد زیرا می‌تواند به n تا معادله دیفرانسیل مرتبه اول تبدیل شود. برای بوجود آوردن این روش‌ها برای حل معادلات مرتبه nام، مساله را به حالت‌های جداگانه تقسیم کرده و سپس برای هر مرحله زمانی روش حل را بکار می‌بریم تا جواب را برای مرحله بعدی بدست آوریم.

روش اویلر برای معادلات دیفرانسیل مرتبه اول

ساده ترین روش برای حل عددی معادلات دیفرانسیل، روش اویلر است که الان توضیح داده می‌شود. معادله دیفرانسیل مرتبه اول زیر را در نظر بگیرید :

در زمان t? شروع می‌کنیم. مقدار y(t?+h) را می‌توان توسط y(t?) بعلاوه زمان تغییر حالت ضرب در شیب تابع تقریب زد. که مشتق y(t) است.

ما این تقریب را y*(t) می‌نامیم.

بنابرین اگر بتوانیم مقدار dy/dt را در زمان t? محاسبه کنیم، می‌توانیم مقدار تقریبی y در زمان t?+h را حدس بزنیم. سپس این مقدار جدید y(t?) را استفاده کرده، دوباره dy/dt را حساب و این کار را تکرار می‌کنیم. به این روش متد اویلر می‌گوییند.

توسط این پیش زمینه ساده روش اویلر برای معادلات دیفرانسیل مرتبه اول بصورت زیر است :

?) در زمان t? شروع کنید، یک مقدار برای h در نظر بگیرید، سپس شرایط ابتدایی y(t?) را حساب کنید. ?) از طریق y(t?) مشتق y(t) را در زمان t=t? حسب کنید. آنرا k? بنامید. این شیب توسط خط قرمز در شکل بالا نشان داده شده‌است.

?) از این مقدار، مقدار تقریبی y*(t?+h) را حساب کنید.

?) قرار دهید t?=t?+h، y(t?)=y*(t?+h) ?) مراحل ? تا ? را آنقدر تکرار کنید تا جواب به دست آید.

روش اویلر برای معادلات دیفرانسیل مرتبه بالاتر

روشی که در بالا بیان شد برای تقریب معادلات دیفرانسیل مرتبه اول کاربرد داشت، ولی بطور واضح نمی‌توان این جواب را برای معادلات دیفرانسیل مراتب بالاتر قبول کرد. ترفندی که در اینجا بکار می‌رود، تقسیم کردن آن به معادلات دیفرانسیل مراتب پایین تر است. این روش «آنالیز حالت‌های متغییر» نامیده می‌شد.

روش Runge – kutta مرتبه دوم

بطور واضح بین درستی و پیچیدگی محاسبات و مقدار انتخاب شده h وابستگی زیادی وجود دارد. بطور کلی هرچه مقدار h کوچک‌تر شود، محاسبات طولانی تر ولی دقیق تر می‌شود. حال اگر مقدار h خیلی کوچک شود، برای اینکه نمی‌توان آنرا به درستی در کامپیوتر نشان داد خطا ایجاد می‌شود. برای سیستم‌های مرتبه بالاتر، تقریب اویلر بسیار سخت است. به همین دلیل، دقت بالاتر و تکنیک‌های با جزییات بیشتر ساخته شد. ما در مورد متدی بحث می‌کنیم که توسط دو ریاضیدان به اسمهای Runge و Kutta ساخته شده‌است.

این تکنیک برای مشتق تابع y(t) در t? از متد اویلر استفاده می‌کند. از k? نیز برای بدست آوردن مقدار اولیه y(t?+h) استفاده می‌کنیم. از y*(t?+h) می‌توانیم مقدار مشتق y(t) را در t?+h حساب کنیم که آنرا k? می‌نامیم. سپس میانگین این دو مشتق را k? می‌نامیم.

روش RK?، تقریب را از طریق تخمین زدن بیشتر این تقریب، از روی فاصله شیب حساب می‌کند. روش اویلر مشتق را در y(t?) حساب کرده و از آن در تقریب y(t?+h) استفاده می‌کند.

بصورت الگوریتم می‌توانیم روش RK? را استفده کنیم :

?) در زمان t? شروع به محاسبات می‌کنیم. ?) در زمان t?، مشتق y(t) را حساب کرده و آنرا k? می‌نامیم.

?) مقدار ابتدایی y*(t?+h) را حساب کرده و فرمول اویلر را استفاده می‌کنیم.

?) از y*(t?+h) مشتق y(t) را در t?+h حساب کرده و آنرا k? می‌نامیم.

?) مقدار جدید y*"(t?+h) را از میانگین k? وk? محاسبه میکنیم.

?) قرار دهید y(t?) = y*"(t+?h) و t? = t?+h ?) مراحل ? تا ? را تکرار کنید تا جواب بدست آید.

نظر شما ()

8:0 عصر چهارشنبه 87/9/6

فرمول اولر

نویسنده: امیررضا طغرلی

فورمول اولر (Euler"s formula)، منتسب به لئونارد اولر، اتحادی است در آنالیز مختلط که رابطه? مابین تابع نمایی مختلط و توابع مثلثاتی را به صورت زیر بیان می‌دارد:

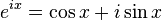
$e^{ix} = \cos x + i\sin x \!$

که در اینجا $e \!$ پایه لگاریتم طبیعی، $i = \sqrt{-1} \!$ واحد موهومی، و متغیر $x \!$ عددی دلخواه و حقیقی بر حسب واحد رادیان است

نظر شما ()

7:59 عصر چهارشنبه 87/9/6

رادیان

نویسنده: امیررضا طغرلی

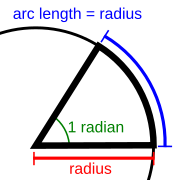
رادیان زاویه مرکزی مقابل با کمانی است از دایره که طول آن با شعاع برابر است. یعنی محیط دایره مساوی $2?$ رادیان و اندازه زاویه نیم صفحه $?$ رادیان و اندازه قائمه $? / 2$ رادیان است.

تبدیل رادیان به درجه

هر رادیان برابر $\frac{180}{\pi}$ درجه است. بنابر این با ضرب $\frac{180}{\pi}$ در رادیان، درجه به دست می‌آید. به عنوان مثال:

$1 \mbox{ rad} = 1 \cdot \frac {180^\circ} {\pi} \approx 57.2958^\circ$

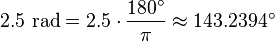
$2.5 \mbox{ rad} = 2.5 \cdot \frac {180^\circ} {\pi} \approx 143.2394^\circ$

و بلعکس: با ضرب $\frac{\pi}{180}$ در درجه، رادیان بدست می آید:

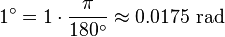
$1^\circ = 1 \cdot \frac {\pi} {180^\circ} \approx 0.0175 \mbox{ rad}$

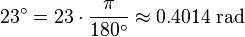
$23^\circ = 23 \cdot \frac {\pi} {180^\circ} \approx 0.4014 \mbox{ rad}$

جدول زیر تبدیل چند زاویه پرکاربرد را نمایش می دهد:

درجه	0°	30°	45°	60°	90°	180°	270°	360°
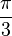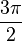رادیان	0	$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$	$\pi\,$	$\frac{3\pi}{2}$	$2\pi\,$

نظر شما ()

< 1 2 3 4 5 >> >

لیست کل یادداشت های این وبلاگ

مطالب طنز
[عناوین آرشیوشده]

[ خانه :: پارسی بلاگ :: مدیریت:: پست الکترونیک :: شناسنامه]

اوقات شرعی


	تعداد بازدید:65028
	امروز:11 دیروز :3 RSS


	درباره خودم
	امیررضا طغرلی


	لوگوی خودم



	لوگوی دوستان



	آرشیو
	تانژانت(ریاضیات) دایره مثلثاتی(ریاضیات) سینوس(ریاضیات) تابع(ریاضیات) گسل زمین شناسی گدازه آتشفشان باکتری ها جدول تناوبی عناصر1 جدول تناوبی عناصر2 عجایب هفت گانه احتمال گسسته(ریاضیات) هندسه ابوالحسن بنی صدر فرمول های مهم مثلثاتی(ریاضیات) قانون کسینوس ها(ریاضیات) فرمول اولر(ریاضیات) رادیان(ریاضیات) حل عددی معادلات دیفرانسیل معمولی(ریاضیات) جبر خطی(ریاضیات) فضای برداری(ریاضیات) دنباله(ریاضیات) تابع نمایی(ریاضیات) بهرام گور کروموزوم و میتوز عدسی ها(فیزیک) قانون کولن(فیزیک) ظرفیت گرمایی(فیزیک) قانون هوک(فیزیک) اخترشناسی1 اخترشناسی2 اخترشناسی3 اخترشناسی4 روباتیک باراک اوباما به روایت تصویر اسفند 1387


	اشتراک