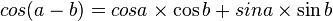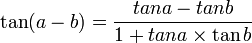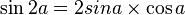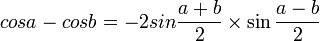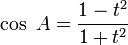امیررضا طغرلی - به وبلاگ خودتون خوش آمدید

7:56 عصر چهارشنبه 87/9/6

قانون کسینوس ها

نویسنده: امیررضا طغرلی

در مثلثات قانون کسینوس‌ که به نام‌ قانون کاشانی هم شناخته می شود و در مورد هر نوع مثلثی صدق می کند به این شکل است:

$c^2 = a^2 + b^2 - 2ab\cos(\gamma) , \,$

$b^2 = c^2 + a^2 - 2ca\cos(\beta) , \,$

$a^2 = b^2 + c^2 - 2bc\cos(\alpha) , \,$

$\cos(\gamma) = \frac{a^2 + b^2 - c^2}{2ab}\ . \,$

نظر شما ()

7:53 عصر چهارشنبه 87/9/6

فرمول های مهم مثلثاتی

نویسنده: امیررضا طغرلی

فرمول های مهم مثلثات برای تبدیل و محاسبه از این قرارند:

$\cos^{2} A + \sin^{2} A = 1 \,$

$\ cos (a+b)=cos a\times\ cos b - sin a\times\ sin b \,$

$\ cos (a-b)=cos a \times\cos b + sin a \times\sin b \,$

$\ sin (a+b)=sin a \times\cos b + cos a \times\sin b \,$

$\ sin (a-b)=sin a \times\cos b - cos a \times\sin b \,$

$\tan(a+b) = \frac{tan a + tan b}{1-tan a\times\tan b}\ \,$

$\tan(a-b) = \frac{tan a - tan b}{1+tan a\times\tan b}\ \,$

$\cos 2a=cos^2 a -sin^2 a=2cos^2 a -1= 1 - 2sin^2 a \,$

$\sin 2a=2sin a\times\cos a \,$

$\cos^2 a=\frac{1}{2}\ (1+cos 2a) \,$

$\sin^2 a=\frac{1}{2}\ (1-cos 2a) \,$

$\ cos a \times\cos b =\frac{1}{2}(cos (a+b)+ cos (a-b))$

$\ sin a \times\sin b =\frac{1}{2}(cos (a-b)- cos (a+b))$

$\ sin a \times\cos b =\frac{1}{2}(sin (a+b)+ sin (a-b))$

$\ cos a +cos b=2 cos\frac{ a+b }{ 2 }\times\cos\frac{ a-b }{2}\ \,$

$\ cos a -cos b=-2 sin\frac{ a+b }{ 2 }\times\sin\frac{ a-b }{2}\ \,$

$\ sin a +sin b=2 sin\frac{ a+b }{ 2 }\times\cos\frac{ a-b }{2}\ \,$

$\ sin a -sin b=2 cos\frac{ a+b }{ 2 }\times\sin\frac{ a-b }{2}\ \,$

چنانچه $t = \tan \frac{A}{2}$ , : آنگاه

$\sin\ A = {{2\,t} \over {1+t^{2}}}$

$\cos\ A = {{1-t^{2}} \over {1+t^{2}}}$

$\tan\ A = {{2\,t}\over {1-t^{2}}}$

فرمول کاشانی که در هر مثلثی صدق می کند

$a^2 = b^2 + c^2 - 2\,b\,c \cdot cos\ A$

نظر شما ()

7:46 عصر چهارشنبه 87/9/6

بهرام گور

نویسنده: امیررضا طغرلی

بهرام پنجم یا بهرامِ گور فرزند یزگرد یکم پادشاه ساسانی بود.او در سال ??? میلادی توانست مدعیان پادشاهی را کنار بزند و بر تخت پادشاهی ایران بنشیند.

پادشاهی

بهرام از کودکی نزد نعمان پسر منذر پادشاه عرب حیره بزرگ شده بود. پس از مرگ یزدگرد، بزرگان شاپور پسر بزرگ وی را که شاه ارمنستان و جانشین پدر بود کشتند و خسرو نامی را که پدرش شاه نبود و خویشی نزدیکی با شاه نداشت بر تخت نشاندند. بهرام با سپاهی که بیشتر از عربها بودند به پایتخت بازگشت و خسرو را شکست داد و بر تخت نشست.

برخورد با بیگانگان

او در شرق هپتالیان را به سختی شکست داد.در غرب با روم صلح کرد و پیمانی با این کشور بست که بر پایه? آن مسیحیان در ایران و زرتشتیان در روم دارای آزادی مذهبی شدند. در این زمان ارمنیان از بهرام خواستار یاری شدند تا شاه آنان آرتاشِس(اردشیر) پسر بهرام شاپور(ورام شاپو) را کنار بگذارند. در سال ??? بهرام چنین کرد و مرزبانی را در ارمنستان بر تخت نشاند.

بهرام گور در فولکور

بهرام پادشاهی دلیر و جنگجو بود. داستان‌های بسیاری را به او نسبت می‌دهند.آوردن کولیان از هند به ایران را از کارهای او می‌دانند. او این کار را برای شادمان کردن مردم انجام داده بود زیرا کولیان نوازندگان و رقصندگان توانایی بودند.او به شکار و باده‌گساری بسیار دلبسته بود.دلبستگی‌اش به شکار گورخر سبب شد که به او لقب بهرام گور را بدهند. همچنین، در برخی از کتاب‌های پارسی سرودن نخستین شعر پارسی را از او می‌دانند که چنین سرود:

منم شیر شلمبه و منم ببر یله

و چنان که هرمان اته شرق‌شناس نامی آلمانی تحقیق کرده‌است، اولین بار که در کودکی با همبازی‌هایش توشله بازی می‌کرد و توشله‌اش همینطور که داشت آهسته آهسته یکراست به طرف چاله‌اش می‌رفت وی از شوق موفقیت و به نیروی ذوق ادبی و احساس شعری قوی که داشت بر زبانش فی البداهه جاری شد که:

غلطان غلطان همی رود تا لب گو* ^[?] ^[?]

همچنین در داستان‌ها چنین انگاشته شده که در جست‌وجوی گوری در ماد در باتلاقی گرفتار آمد و باتلاق او را در خود فروخورد. همچنین، نویسندگان زرتشتی زمان او را زمان آرامش و آشتی می‌دانند و زمانی که دیوان از ترس او پنهان شدند.

حکیم نظامی گنجوی در هفت پیکر (بهرامنامه) داستان بهرام را از بدو تولد تا مرگ رازگونه‌اش بیان می‌کند.

شاهنشاهان ساسانی

اردشیر یکم (اردشیر بابکان) • شاپور یکم • هرمز یکم • بهرام یکم • بهرام دوم • بهرام سوم • نرسی • هرمز دوم • آذرنرسی • شاپور دوم • اردشیر دوم • شاپور سوم • بهرام چهارم • یزدگرد یکم • بهرام پنجم (بهرام گور) • یزدگرد دوم • هرمز سوم • پیروز یکم • بلاش • قباد یکم • جاماسب • قباد یکم • خسرو یکم (خسرو انوشیروان) • هرمز چهارم (ترک‌زاد) • بهرام ششم • خسرو دوم (خسرو پرویز) • قباد دوم (شیرویه) • اردشیر سوم • شهربراز • خسرو سوم • جوانشیر • پوراندخت • گشناسب بنده • آزرمی دخت • هرمز پنجم • پیروز دوم • خسرو پنجم • یزدگرد سوم

شاهنشاهان ساسانی

اردشیر یکم (اردشیر بابکان) • شاپور یکم • هرمز یکم • بهرام یکم • بهرام دوم • بهرام سوم • نرسی • هرمز دوم • آذرنرسی • شاپور دوم • اردشیر دوم • شاپور سوم • بهرام چهارم • یزدگرد یکم • بهرام پنجم (بهرام گور) • یزدگرد دوم • هرمز سوم • پیروز یکم • بلاش • قباد یکم • جاماسب • قباد یکم • خسرو یکم (خسرو انوشیروان) • هرمز چهارم (ترک‌زاد) • بهرام ششم • خسرو دوم (خسرو پرویز) • قباد دوم (شیرویه) • اردشیر سوم • شهربراز • خسرو سوم • جوانشیر • پوراندخت • گشناسب بنده • آزرمی دخت • هرمز پنجم • پیروز دوم • خسرو پنجم • یزدگرد سوم

نظر شما ()

7:47 عصر شنبه 87/9/2

هندسه

نویسنده: امیررضا طغرلی

هِندِسه مطالعه انواع روابط طولی و اشکال و خصوصیات آن‌ها است. این دانش همراه با حساب یکی از دو شاخه‌ قدیمی ریاضیات است.

واژه هندسه عربی شده واژه «اندازه» در فارسی است. در زبان انگلیسی به آن geometry و در زبان فرانسه به آن géométrie می‌گویند که هردو از ????????? (گئومتریا) در زبان یونانی آمده که به معنای اندازه‌گیری زمین است

تاریخچه هندسه:

احتمالاً بابلیان و مصریان کهن نخستین کسانی بودند که اصول هندسه را کشف کردند. در مصر هر سال رودخانه نیل طغیان می‌کرد و نواحی اطراف رودخانه را سیل فرا می‌گرفت. این رویداد تمام علایم مرزی میان املاک را از بین می‌‌برد و لازم می‌‌شد دوباره هر کس زمین خود را اندازه‌گیری و مرزبندی کند. مصریان روش علامت‌گذاری زمین‌ها با تیرک و طناب‌ را ابداع کردند. آنها تیرکی را در نقطه‌ای مناسب در زمین فرو می‌‌کردند و تیرک دیگری در جایی دیگر نصب می‌شد و دو تیرک با طنابی که مرز را مشخص می‌‌ساخت به یکدیگر متصل می‌شدند. با دو تیرک دبگر زمین محصور شده و محلی برای کشت یا ساختمان سازی مشخص می‌شد.

در آغاز هندسه برپایه دانسته‌های تجربی پراکنده‌ای در مورد طول و زاویه و مساحت و حجم قرار داشت که برای مساحی و ساختمان و نجوم و برخی صنایع دستی لازم می‌شد. بعضی از این دانسته‌ها بسیار پیشرفته بودند مثلاً هم مصریان و هم بابلیان قضیه فیثاغورث را ???? سال قبل از فیثاغورث می‌شناختند.

یونانیان دانسته‌های هندسی را مدون کردند و بر پایه‌ای استدلالی قراردادند. برای آنان هندسه مهم‌ترین دانش‌ها بود و موضوع آن را مفاهیم مجردی می‌دانستند که اشکال مادی فقط تقریبی از آن مفاهیم مجرد بود. در سال ??? قبل از میلاد مسیح، یک آموزگار اهل ایونیا (که در روزگار ما بخشی از ترکیه به‌شمار می‌رود) به نام طالس، چند گزاره یا قضیه هندسی را به صورت استنتاجی ثابت کرد. او آغازگر هندسه ترسیمی بود. روش استنتاجی روشی است علمی (بر خلاف روش استقرایی) که در آن مساله‌ای به وسیله‌ی قضا‌یا و حکمها ثابت می گردد. فیثاغورث که او نیز اهل ایونیا و احتمالاً از شاگردان طالس بود توانست قضیه‌ای را که به‌نام او مشهور است اثبات (ریاضی) کند. البته او واضع این قضیه نبود.

اما دانشمندی به نام اقلیدس که در اسکندریه زندگی می‌‌کرد، هندسه را به صورت یک علم بیان نمود. وی حدود سال ??? پیش از میلاد مسیح، تمام نتایج هندسی را که تا آن زمان شناخته بود، گرد آورد و آنها را به طور منظم، در یک مجموعه ?? جلدی قرار داد. این کتابها که اصول هندسه نام داشتند، به مدت ? هزار سال در سراسر دنیا برای مطالعه هندسه به کار می‌‌رفتند.

براساس این قوانین، هندسه اقلیدسی تکامل یافت. هر چه زمان می‌‌گذشت، شاخه‌های دیگری از هندسه توسط ریاضیدانان مختلف، توسعه می‌‌یافت. امروزه در بررسی علم هندسه انواع مختلف این علم را نظیر هندسه تحلیلی و مثلثات، هندسه غیر اقلیدسی و هندسه فضایی مطالعه می‌‌کنیم.

خدمت بزرگی که یونانیان در پیشرفت ریاضیات انجام دادند این بود که آنان احکام ریاضی را به جای تجربه بر استدلال منطقی استوار کردند. قبل از اقلیدس، فیثاغورث (572-500 ق.م) و زنون (490 ق.م.) نیز به پیشرفت علم ریاضی خدمت بسیار کرده بودند.

در قرن دوم قبل از میلاد ریاضیدانی به نام هیپارک، مثلثات را اختراع کرد. وی نخستین کسی بود که تقسیم بندی بابلی‌ها را برای پیرامون دایره پذیرفت. به این معنی که دایره را به ??? درجه و درجه را به ?? دقیقه و دقیقه را به ?? قسمت برابر تقسیم نمود و جدولی براساس شعاع دایره به دست آورد که وترهای بعضی قوسها را به دست می‌‌داد و این قدیمی‌ترین جدول مثلثاتی است که تاکنون شناخته شده است.

بعد از آن دانشمندان هندی موجب پیشرفت علم ریاضی شدند. در سده پنجم میلادی آپاستامبا، در سده ششم، آریابهاتا، در سده هفتم، براهماگوپتا و در سده نهم، بهاسکارا در پیشرفت علم ریاضی بسیار مؤثر بودند.

تقسیم بندی هندسه

هنـدسه مقـدماتی به دو قسمت تقسیـم می‌گردد:

در هندسه مسطحه، اشکالی مورد مطالعه قرار می‌‌گیرند که فقط دو بعد دارند، هندسه فضایی، مطالعه اشکال هندسی سه بعدی است. این بخش از هندسه در مورد اشکال سه بعدی چون مکعبها ،استوانه ها، مخروط ها، کره‌ها و غیره است.

نظر شما ()

7:40 عصر شنبه 87/9/2

احتمال گسسته

نویسنده: امیررضا طغرلی

پیشینه‌ی نظریه‌ی احتمال، به قرن هفدهم میلادی و مطالعات بلیز پاسکال روی اعداد ظاهر شده بر تاس‌ها برمی‌گردد. پس از او لاپلاس، احتمال را به صورت نسبت پیشامدهای مطلوب به کل پیشامدها تعریف کرد. برای مثال احتمال آمدن عدد زوج، هنگام انداختن یک تاس سالم، برابر است با 3 (یعنی تعداد حالت‌هایی که ممکن است عدد زوج بیاید یا به تعبیر دیگر 2، 4 یا 6 ظاهر شود) بخش بر 6 (یعنی کل حالت‌هایی که ممکن است با انداختن تاس ظاهر شود یا به تعبیر دیگر آمدن 1، 2، 3، 4، 5 یا 6) که برابر می‌شود با ${3\over 6}$ یا ${1\over2}$ .

نظریه‌ی احتمال

چند تعریف

برای ادامه‌ی بحث، لازم است که ابتدا چند واژه را تعریف کنیم:

آزمایش تصادفی: یک آزمایش که نتیجه‌ی آن به هیچ‌وجه قابل پیش‌بینی نباشد یا اصطلاحاً تصادفی باشد؛ مثل انداختن تاس یا سکه.
فضای نمونه^[?]‌: مجموعه‌ی کل نتیجه‌هایی که ممکن است از یک آزمایش تصادفی حاصل شود؛ مثلاً در آزمایش انداختن تاس فضای نمونه به صورت ${1,2,3,4,5,6}$ است.
پیشامد^[?]: به هریک از زیرمجموعه‌های فضای نمونه‌ یک پیشامد می‌گویند؛ مثلاً ${2,4,6}$ یک پیشامد در آزمایش انداختن تاس است.
فضای نمونه‌ی هم‌شانس^[?]: در صورتی که همه‌ی اعضای فضای نمونه‌ شانس برابری برای ظاهر شدن داشته باشند یا به عبارت دیگر، شانس تمام اعضا یکسان باشد، این فضای نمونه را هم‌شانس می‌خوانیم. مثلاً آزمایش انداختن تاس سالم^[?] در فضای هم‌شانس است.

احتمال در فضای متناهی

اگر فضای نمونه‌ی ما هم‌شانس و دارای تعداد اعضای متناهی باشد، برای محاسبه‌ی احتمال وقوع یک پیشامد، فرمول لاپلاس را به کار می‌گیریم.

$p={|E|\over |S|}$

یا به عبارت دیگر، احتمال وقوع یک پیشامد برابر است با نسبت اندازه‌ی پیشامد به اندازه‌ی فضای نمونه. برای مثال اگر آزمایش انداختن تاس سالم را در نظر بگیریم که دارای فضای نمونه‌ی هم‌شانس با اندازه‌ی متناهی است، با توجه به آن‌چه پیش‌تر گفته شد، احتمال آمدن عدد 6، برابر است با اندازه پیشامد (یعنی اندازه‌ی ${6}$ که 1 است) بخش بر اندازه‌ی فضای نمونه (یعنی اندازه‌ی ${1,2,3,4,5,6}$ که 6 است). به این ترتیب احتمال آمدن عدد 6، برابر با $1\over 6$ محاسبه می‌شود.

احتمال پیشامدهای مرکب

گاهی می‌خواهیم با داشتن احتمال چند پیشامد، بتوانیم احتمال مجموعه‌ی حاصل از اعمال جبر مجموعه‌ها بر آن‌ها را نیز محاسبه کنیم. دو مورد از این موارد مهم‌تر است:

احتمال مکمل یک پیشامد: مکمل یک پیشامد زمانی اتفاق می‌افتد که خود آن پیشامد اتفاق نیفتد. به عبارت دیگر ما می‌خواهیم احتمال رخ ندادن یک پیشامد را حساب کنیم. از آن‌جا که پیشامد زیرمجموعه‌ای از فضای نمونه است، مکمل آن، مجموعه‌ی اعضای فضای نمونه‌ است که در پیشامد مورد نظر ما نیستند. به این ترتیب با توجه به فرمول لاپلاس، رابطه‌ی زیر برای محاسبه‌ی احتمال مکمل یک پیشامد، با داشتن احتمال خود آن پیشامد به دست می‌آید:

$p(\bar{E})=1-p(E)$

با توجه به آن‌چه گفته شد اثبات این رابطه بسیار ساده است.

احتمال اجتماع^[?] دو پیشامد: همان‌طور که از مفهوم اجتماع مجموعه‌ها برمی‌آید، وقوع اجتماع دو پیشامد به معنی آن است که حداقل یکی از این دو پیشامد اتفاق بیفتد. برای محاسبه‌ی احتمال اجتماع دو پیشامد، با فرض داشتن احتمال خود آن‌ها و احتمال اشتراک^[?]شان، رابطه‌ی زیر را داریم:

$p(E\cup F)=p(E)+p(F)-p(E\cap F)$

اثبات این رابطه با دانستن این‌که $|E\cup F|=|E|+|F|-|E\cap F|$ میسر است.

تخصیص احتمال

تا این‌جا بیش‌تر درباره‌ی آزمایش‌ها و فضاهای نمونه‌ای بحث کردیم که هم‌شانس هستند. با این‌همه، بسیاری از آزمایش‌ها در فضای هم‌شانس اتفاق نمی‌افتند و لذا برای محاسبه‌ی احتمال آن‌ها نمی‌توان به سادگی فرمول لاپلاس را به کار برد.

برای حل این مشکل، راه‌حل تخصیص احتمال^[?] را به این ترتیب به کار می‌بریم: به تک‌تک اعضای فضای نمونه‌ احتمالی نسبت می‌دهیم که از دو قانون زیر پیروی کند:

مقدار هر یک از این احتمال‌ها باید بین صفر و یک باشد؛ به عبارت دیگر برای هر $s\in S$ داشته باشیم:

$0\leq p(s)\leq 1$

مجموع مقدار احتمال‌های تخصیص‌داده‌شده، برابر 1 باشد؛ به عبارت دیگر داشته باشیم:

$\sum_{s\in S} p(s)=1$

به تابع احتمال p، تابع توزیع احتمال^[?] می‌گوییم.

اگر تابع احتمال به هر عضو فضای نمونه‌، مقدار یکسانی نسبت دهد، آن را توزیع یک‌نواخت^[?] می‌خوانیم.

روشن است که با توجه به آن‌چه در این‌جا تعریف کردیم، احتمال وقوع یک پیشامد برابر است با مجموع احتمال اعضایی از فضای نمونه که در آن پیشامد حضور دارند.

احتمال شرطی و استقلال پیشامدها

فرض کنید خانواده‌ای دو فرزند دارد. می‌خواهیم بدانیم اگر فرزند اول پسر باشد، با چه احتمالی فرزند دوم دختر خواهد بود؟ برای حل چنین مسئله‌ای از رابطه‌ی احتمال شرطی^[??] استفاده می‌کنیم که به شکل زیر است:

$p(E|F)={p(E\cap F)\over p(F)}$

یا به عبارت دیگر احتمال وقوع E، اگر F اتفاق افتاده باشد، برابر است با نسبت احتمال اشتراک E و F به احتمال F.

حال اگر این دو پیشامد از هم مستقل^[??] باشند، روشن است که وقوع E ارتباطی با وقوع F نخواهد داشت یا به تعبیر دیگر $p (E | F)$ همان $p (E)$ خواهد بود.

به این ترتیب می‌توانیم دو پیشامد E و F را مستقل بدانیم، در صورتی که:

$p(E\cap F)=p(E)p(F)$

توزیع احتمال دوجمله‌ای

یک آزمایش تصادفی بسیار مشهور، موسوم به آزمایش برنولی^[??]، به این شکل تعریف می‌شود:

آزمایشی تصادفی که در هر بار انجام آن تنها یا پیروزی اتفاق می‌افتد یا شکست.

با توجه به این آزمایش، در صورتی که n بار آزمایش برنولی انجام شود، و این آزمایش‌ها از هم مستقل باشند و احتمال پیروزی نیز p باشد، آن‌گاه تابع توزیع احتمال، مشهور به توزیع احتمال دوجمله‌ای^[??] خواهیم داشت که به صورت ${n\choose k}p^k(1-p)^{n-k}$ است (k تعداد پیروزی‌هاست).

علت این‌ نام‌گذاری، شباهت فوق‌العاده‌ی رابطه‌ی به‌دست‌آمده با رابطه‌ی بسط دوجمله‌ای نیوتن است.

توزیع احتمال هندسی

اگر آزمایش برنولی (که در بخش قبل معرفی شد) آن‌قدر تکرار شود تا پیروزی به دست آید، در این صورت توزیع احتمالی به دست می‌آید که به توزیع احتمال هندسی^[??] مشهور است. در این حالت فضای نمونه، تعداد اعضای نامتناهی دارد و هر عضو را می‌شود یک توالی^[??] در نظر گرفت. تابع توزیع احتمال در این حالت به شکل زیر است (p احتمال پیروزی و k تعداد دفعات لازم برای تکرار آزمایش است تا پیروزی حاصل شود):

p (1 ? p) k ? 1

توجه کنید که تعریف این توزیع را می‌توانستیم به این ترتیب انجام دهیم که آن‌قدر آزمایش تکرار شود تا نتیجه‌ی شکست به دست آید. اگر تعریف به این شکل باشد، کافی است جای p و 1-p را در رابطه‌ی به‌دست‌آمده عوض کنیم.

متغیر تصادفی، امیدریاضی و واریانس

در این بخش به معرفی سه تابع بسیار مهم مرتبط با احتمال می‌پردازیم. این تابع‌ها، کاربردهای وسیعی در نظریه‌ی احتمال و مباحث آماری دارند.

متغیر تصادفی

متغیر تصادفی^[??]، تابعی است که از فضای نمونه بر اعداد حقیقی تعریف شده است؛ یعنی هر عضو از فضای نمونه را به یک عدد حقیقی مربوط می‌کند. متغیر تصادفی را معمولاً با X نشان می‌دهند. (اشتباه نکنید! متغیر تصادفی، نه متغیر است و نه تصادفی! این تنها یک نام‌گذاری است).

مثلاً فرض کنید که خانواده‌ای دو فرزند دارد. به این ترتیب فضای نمونه‌ی حالت‌های ممکن برای این جنسیت دو فرزند به صورت {(پ،د)و(د،پ)و(د،د)و(پ،پ)} خواهد بود. حال فرض کنید متغیر تصادفی X قرار است تعداد فرزندان دختر را مشخص کند. به این ترتیب خواهیم داشت:

0=(پ،پ)X 1=(پ،د)X 1=(د،پ)X 2=(د،د)X

همان‌طور که برای یک آزمایش تصادفی، توزیع احتمال تعریف کردیم، می‌توانیم برای متغیر تصادفی نیز تابع توزیع احتمال تعریف کنیم که با (p(X=r نموده می‌شود. مثلاً در مورد همان مثال بالا، تابع توزیع احتمال به این شکل درمی‌آید:

$p(X=0)={1\over4}$ $p(X=1)={1\over2}$ $p(X=2)={1\over4}$

حال می‌توانیم دومین تابع را معرفی کنیم.

امیدریاضی

امیدریاضی^[??]، در حقیقت یک نوع میانگین‌گیری از متغیر تصادفی است. یعنی این‌که اگر یک آزمایش را بی‌نهایت‌بار تکرار کنیم و از مقدارهای متغیر تصادفی مرتبط با نتایج میانگین بگیریم، چه عددی به دست خواهد آمد. معرفی دقیق ریاضی این تابع کمک بیش‌تری خواهد کرد:

$E(X)=\sum_{s\in S} p(s)X(s)$

برای نمونه، اگر همان مثال گفته شده در بخش قبل را در نظر بگیریم، امیدریاضی تعداد دختران یک خانواده با دو فرزند به صورت زیر خواهد بود:

$0\times{1\over4}+1\times{1\over2}+2\times{1\over4}=1$

یکی از مهم‌ترین ویژگی‌های تابع امیدریاضی، خطی بودن آن است؛ یعنی اگر n متغیر تصادفی به صورت 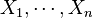$X_1,\cdots,X_n$ داشته باشیم، تساوی زیر برقرار خواهند بود:

$E(X_1+\cdots+X_n)=E(X_1)+\cdots+E(X_n)$

E (a X 1 + b) = a E (X 1) + b

برای ادامه‌ی بحث، بد نیست تعریف زیر را انجام دهیم:

دو متغیر تصادفی X و Y را مستقل می‌خوانیم در صورتی که برای هر $a,b\in \mathbb{R}$ داشته باشیم احتمال X=a و Y=b برابر است با حاصل‌ضرب احتمال X=a در احتمال Y=b.

با توجه به این تعریف، می‌توان ثابت کرد که حکم مهم زیر برقرار است:

اگر X و Y دو متغیر تصادفی مستقل باشند، آن‌گاه خواهیم داشت (E(XY)=E(X)E(Y.

اگر به یاد داشته باشید در مبحث قبل، توزیع احتمال دوجمله‌ای و هندسی را تعریف کردیم. محاسبات نشان می‌دهند که امیدریاضی توزیع احتمال دوجمله‌ای برابر $n p$ و امیدریاضی توزیع احتمال هندسی برابر $1\over p$ خواهد بود.

حال به معرفی آخرین تابع می‌پردازیم که در محاسبات آماری جایگاه ویژه‌ای دارد.

واریانس

واریانس^[??] در محاسبات آماری، یک معیار برای سنجش میزان پراکندگی داده‌ها از میانگین است. ما در این مباحث، امیدریاضی را مشابه میانگین در نظر گرفتیم و به این ترتیب واریانس را چنین تعریف می‌کنیم:

اگر X متغیر تصادفی روی فضای نمونه‌ی S باشد، واریانس X برابر خواهد بود با:

$V(X)=\sum_{s\in S} (X(s)-E(X))^2p(s)$

حکم بسیار مهمی که در محاسبات بسیار راه‌گشاست و از تعریف نتیجه می‌شود به قرار زیر است:

اگر متغیر تصادفی X روی فضای نمونه‌ی S تعریف شده باشد، واریانس از رابطه‌ی زیر نیز به دست می‌آید:

V (X) = E (X 2) ? E (X) 2

در این‌جا مقصود از $X 2$ این است که مقدارهای متغیر تصادفی را به توان 2 برسانیم.

مثلاً برای محاسبه‌ی واریانس متغیر تصادفی تعداد فرزندان دختر در یک خانواده‌ با دو فرزند (که در بخش‌های قبل توزیع احتمال و امیدریاضی آن به دست آمد)، باید به این ترتیب عمل کنیم:

${1\over4}(0-1)^2+{1\over2}(1-1)^2+{1\over4}(2-1)^2={1\over2}$

واریانس مجموع چند متغیر تصادفی مستقل را می‌توان برحسب واریانس تک‌تک این متغیرها حساب کرد:

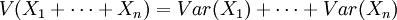
$V(X_1+\cdots+X_n)=Var(X_1)+\cdots+Var(X_n)$

تأکید می‌کنیم که این حکم فقط در صورتی قابل استفاده است که متغیرها مستقل باشند.

نظر شما ()

7:28 عصر شنبه 87/9/2

جدول تناوبی عناصر 2

نویسنده: امیررضا طغرلی

کد رنگ برای اعداد اتمی:

عناصر شماره گذاری شده با رنگ آبی ، در دمای اتاق مایع هستند؛
عناصر شماره گذاری شده با رنگ سبز ، در دمای اتاق بصورت گاز می‌باشند؛
عناصر شماره گذاری شده با رنگ سیاه، در دمای اتاق جامد هستند.
عناصر شماره گذاری شده با رنگ قرمز ترکیبی بوده و بطور طبیعی یافت نمی‌شوند(همه در دمای اتاق جامد هستند.)
عناصر شماره گذاری شده با رنگ خاکستری ، هنوز کشف نشده‌اند (و بصورت کم رنگ نشان داده شده‌اند تا گروه شیمیایی را که در آن قرار می‌گیرند، مشخص نماید.(

و می‌توانید دراین کلید واژه جدول تناوبی برای تشدید مغناطیسی را بیابید.

تعداد لایه الکترون در یک اتم تعیین کننده ردیفی است که در آن قرار می‌گیرد. هر لایه به زیرلایه‌های متفاوتی تقسیم می‌شود، که هر اندازه عدد اتمی افزایش می‌یابد، این لایه‌ها به ترتیب زیر:

1s

2s           2p

3s           3p

4s        3d 4p

5s        4d 5p

6s     4f 5d 6p

7s     5f 6d 7p

8s  5g 6f 7d 8p

...

براساس ساختار جدول پر می‌شوند. از آنجائیکه الکترونهای خارجی‌ترین لایه، خواص شیمیایی را تعیین می‌نمایند، این لایه‌ها در میان گروهای یکسان مشابه‌اند.عناصر همجوار با یکدیگر در یک گروه، علیرغم اختلاف مهم در جرم، دارای خواص فیزیکی مشابه هستند. عناصر همجوار با یکدیگر در یک ردیف دارای جرم‌های مشابه ولی خواص متفاوت هستند.

برای مثال، عناصر بسیار نزدیک به نیتروژن (N) در ردیف دوم کربن(C) و اکسیژن(O) هستند. علیرغم تشابه آنها در جرم (که بصورت ناچیزی در واحد جرم اتمی تفاوت دارند)، دارای خواص بینهایت متفاوتی هستند، همانطور که با بررسی فرمهای دیگر می‌توان ملاحظه نمود: اکسیژن دو اتمی یک کاز است که سوختن را تشدید می‌نماید، نیتروژن دو اتمی یک گاز است که سوختن را تشدید نمی‌کند، و کربن یک جامد است که می‌تواند سوزانده شود(بله، می‌توان الماس را سوزاند!).

در مقایسه، عناصر بسیار نزدیک به کلر (Cl) در گروه یکی مانده به آخر در جدول (هالوژن‌ها) فلوئور(F) و برم(Br) هستند. علیرغم تفاوت فاحش جرم آنها در گروه، فرمهای دیگر آنها دارای خواص بسیار مشابه هستند: آنها بسیار خورنده (بدین معنی که تمایل خوبی برای ترکیب با فلزات، برای تشکیل نمک هالاید فلز)؛ کلر و فلوئور گاز هستند، درحالیکه برم یک مایع با تبخیر بسیار کم است؛ کلر و برم بسیار رنگی هستند.

نظر شما ()

7:27 عصر شنبه 87/9/2

جدول تناوبی عناصر1

نویسنده: امیررضا طغرلی

جدول تناوبی عنصرهای شیمیایی‏، نمایشی از عنصرهای شیمیایی شناخته شده‌است که بر اساس ساختار الکترونی مرتب گردیده‌است به‌گونه‌ای که بسیاری از ویژگی‌های شیمیایی عنصرها به صورت منظم در طول جدول تغییر می‌کنند.

جدول اولیه بدون اطلاع از ساختار داخلی اتم‌ها ساخته شد: اگر عناصر را بر حسب جرم اتمی آنها مرتب نمائیم، و آنگاه نمودار خواص معین دیگر آنها را بر حسب جرم اتمی رسم نمائیم، می‌توان نوسان یا تناوب این خواص را بصورت تابعی از جرم اتمی مشاهده نمود. نخستین کسی که توانست این نظم را مشاهده نماید، یک شیمیدان آلمانی به نام یوهان ولفگانگ دوبراینر بود. او متوجه تعدادی تثلیث از عناصر مشابه شد:

نمونه تثلیث‌ها
عنصر	جرم اتمی	چگالی
Cl	35.5	1.56 g/L
Br	79.9	3.12 g/L
I	126.9	4.95 g/L

Ca	40.1	1.55 g/cm³
Sr	87.6	2.6 g/cm³
Ba	137	3.5 g/cm³

و به دنبال او، شیمیدان انگلیسی جان نیولندز متوجه گردید که عناصر از نوع مشابه در فاصله‌های هشت تایی یافت می‌شوند، که آنها را با نت‌های هشتگانه موسیقی شبیه نمود، هرچند که قانون نت‌های او مورد تمسخر معاصرین او قرار گرفت. سرانجام شیمیدان آلمانی لوتار مَیر و شیمیدان روسی دمیتری مندلیف تقریباً بطور هم‌زمان اولین جدول تناوبی را، با مرتب نمودن عناصر بر حسب جرمشان، توسعه دادند (ولی مندلیف تعداد کمی از عناصر را خارج از ترتیب صریح جرمی، برای تطابق بهتر با خواص همسایگانشان رسم نمود – این کار بعدها با کشف ساختار الکترونی عناصر در اواخر سده نوزدهم و آغاز سده بیستم توجیه گردید).

فهرست عناصر بر پایه نام، علامت اختصاری و عدد اتمی موجود است. شکل زیر جدول تناوبی عناصر شناخته شده را نمایش می‌دهد. هر عنصر با عدد اتمی و علامتهای شیمیایی. عناصر در یک ستون («گروه») از لحاظ شیمیایی مشابه می‌باشند.

گروه

دوره

1
H

2
He

3
Li

4
Be

5
B

6
C

7
N

8
O

9
F

10
Ne

11
Na

12
Mg

13
Al

14
Si

15
P

16
S

17
Cl

18
Ar

19
K

20
Ca

21
Sc

22
Ti

23
V

24
Cr

25
Mn

26
Fe

27
Co

28
Ni

29
Cu

30
Zn

31
Ga

32
Ge

33
As

34
Se

35
Br

36
Kr

37
Rb

38
Sr

39
Y

40
Zr

41
Nb

42
Mo

43
Tc

44
Ru

45
Rh

46
Pd

47
Ag

48
Cd

49
In

50
Sn

51
Sb

52
Te

53
I

54
Xe

55
Cs

56
Ba

71
Lu

72
Hf

73
Ta

74
W

75
Re

76
Os

77
Ir

78
Pt

79
Au

80
Hg

81
Tl

82
Pb

83
Bi

84
Po

85
At

86
Rn

87
Fr

88
Ra

103
Lr

104
Rf

105
Db

106
Sg

107
Bh

108
Hs

109
Mt

110
Ds

111
Rg

112
Uub

113
Uut

114
Uuq

115
Uup

116
Uuh

117
Uus

118
Uuo

* لانتانیدها

57
La

58
Ce

59
Pr

60
Nd

61
Pm

62
Sm

63
Eu

64
Gd

65
Tb

66
Dy

67
Ho

68
Er

69
Tm

70
Yb

** آکتینیدها

89
Ac

90
Th

91
Pa

92
U

93
Np

94
Pu

95
Am

96
Cm

97
Bk

98
Cf

99
Es

100
Fm

101
Md

102
No

در اینجا روشهای دیگر برای نمایش جدول ارائه شده‌اند: جدول استاندارد - جدول جایگزین - جدول ضد - جدول بزرگ - جدول عظیم - جدول عریض - جدول توسعه یافته - جدول ساختاری - فلزات و غیر فلزات

نظر شما ()

7:22 عصر شنبه 87/9/2

باکتری ها

نویسنده: امیررضا طغرلی

باکتریها گروهی از موجودات تک یاخته‌ای ذره بینی هستند که پوشش بیرونی نسبتاً ضخیمی آنها را احاطه کرده است. این موجودات ساختار ساده‌ای دارند و به گروه پروکاریوت‌ها تعلق دارند.

باکتری‌ها متنوع‌ترین و مهم‌ترین میکروارگانیسمها هستند. تعداد کمی از آنها در انسان و حیوانات و گیاهان بیماریزا است. بطور کلی بدون فعالیت آنها، حیات بر روی زمین مختل می‌گردد. بطور یقین یوکاریوتها از موجودات زنده باکتری مانند بوجود آمده‌اند. نظر به اینکه باکتریها ساختمان ساده‌ای داشته و می‌توان به آسانی بسیاری از آنها را در شرایط آزمایشگاه کشت داد و تحت کنترل درآورد، میکروب شناسان مطالعه وسیعی درباره فرایندهای حیاتی آنها انجام داده‌اند.

باکتریها دارای هسته بدون غشا و هستک هستند و اجزای آن در سیتوپلاسم پراکنده‌اند. کروموزمهای غیر مشابه و جداگانه در آنها وجود ندارد. در باکتریها، واکوئل دیده نمی‌شود. بیشتر آنها بدون کلروفیل هستند و دگرگشت (متابولیسم) خود را از راه شیمیوسنتز انجام می‌دهند. تولید مثل به دو صورت جنسی (آمیختگی) و غیر جسمی و جوانه زدن، قطعه قطعه شدن و تقسیم دوتایی صورت می‌گیرد.

یاخته‌های باکتری اشریشیا کولی با بزرگنمایی ??????

تاریخچه

اینکه پروکاریوتها و یا یوکاریوتها کدام یک زودتر بر روی کره زمین ظاهر شده‌اند، کاملاً مشخص نیست. اما مطالعات تفاوتهای ژنتیکی بین یوباکتری ها، آرکی‌باکتری‌ها و یوکاریوت‌ها نشان می‌دهد که هر سه گروه از دنیای مشترکی مشتق شده‌اند. شکل باکتریها بر اساس شکل به 6 گروه تقسیم می‌شود. پنج گروه اول را باکتریهای پست و گروه ششم را باکتریهای عالی گویند.

باکتریهای پست

این باکتریها تک یاخته‌ای بوده و اگر کروی یا بیضوی باشند، کوکوس و اگر میله‌ای شکل یا دراز باشند، باسیل و اگر خمیده باشند ویبریون و چنانچه مارپیچی شکل و غیرقابل انعطاف باشند، اسپریل و اگر فنری و قابل انعطاف باشند، اسپیروکت نامیده می‌شوند.

باکتریهای عالی یا رشته‌ای

این باکتریها رشته مانند و اغلب غلاف دار هستند و اغلب اوقات شاخه‌های حقیقی ایجاد کرده، میسلیوم تشکیل می‌دهند و چون تشکیلات منشعب ایجاد می‌کنند، لذا اکتینومیست نامیده می‌شوند. بنابراین باکتریها از نظر شکل به 6 گروه گرد، دراز، خمیده، مارپیچی، فنری و منشعب تقسیم می‌شوند.

نحوه تقسیم و طرز قرار گرفتن باکتریها

دیپلوکوکوس تقسیم فقط در یک سطح انجام می‌گیرد و باکتریها دو به دو، به یکدیگر اتصال دارند.

استرپتوکوک تقسیمات یاخته‌ای در یک سطح انجام می‌شود و چند باکتری بدنبال هم قرار می‌گیرند.

تتراد اگر تقسیم در دو سطح عمود بر هم باشد اشکال چهارتایی بوجود می‌آید.

سارسین تقسیم یاخته در سه سطح عمود بر هم انجام می‌شود و توده‌های هشت تایی شبیه پاکت پستی بوجود می‌آید.

استا فیلوکوک تقسیمات یاخته بطور نامنظم در سطوح مختلف انجام می‌گیرد و اشکالی شبیه به خوشه انگور بوجود می‌آید.

ساختار باکتریها

پوشینه در بعضی از باکتریها، غلاف ژلاتینی چسبناکی دیواره اسکلتی را احاطه کرده است که توسط باکتریها ساخته شده و به خارج ترشح می‌گردد و جنس پوشینه بیشتر از پلی ساکاریدها همراه با مواد دیگر است.

تاژک از واحدهای پروتئینی به نام فلاژین تشکیل شده و قابل ترمیم بوده و وسیله حرکت باکتری هستند. معمولاً طول آن چند برابر طول باکتری است. آرایش تاژک در باکتریهای تاژکدار بصورت تک تاژکی، دو تاژکی، چند تاژکی سطحی است.

تار به دو صورت جنسی و چسبنده وجود دارد و در عمل تحرک بی تأثیر است.

دیواره در بیرون غشای پلاسمایی بوده و سبب استحکام باکتری شده و به آن شکل می‌دهد. وجود دیواره برای رشد و تقسیم باکتریها لازم است.

غشای سیتوپلاسمی به صورت پرده نازکی در داخل دیواره باکتری قرار دارد و متشکل از مولکولهای چربی و پروتئینی است.

مزوزومها از فرورفتگی غشای سیتوپلاسمی به درون سیتوپلاسم حاصل می‌شود و اغلب در محل تقسیم دیواره وجود دارند و در عمل تقسیم DNA، تقسیم یاخته‌ای و تبدیل باکتری به هاگ دخالت می‌کنند.

اجزای سیتوپلاسم ریبوزمها مواد ذخیره‌ای ماده زمینه کروماتومور ماده ژنتیکی که DNA آنها غالبا به صورت یک کروموزوم تاخورده و بهم فشرده است.

تولیدمثل باکتری

باکتریها به روشهای تقسیم مستقیم، آمیختگی، قطعه قطعه شدن یا به‌وسیله کنیدی و همچنین جوانه زدن تکثیر می‌یابند. برخی باکتریها توانایی ایجاد هاگ درونی را دارند. هاگ سبب مقاومت باکتری در برابر عوامل نامساعد محیط می‌شود. هر باکتری فقط یک هاگ می‌سازد و از هر هاگ یک باکتری بوجود می‌آید.

نظر شما ()

7:11 عصر شنبه 87/9/2

گدازه

نویسنده: امیررضا طغرلی

گُدازه گونه‌ای تفتال است که بر اثر فعالیت‌های آتشفشانی به سطح زمین راه یابد. به تعریف دیگر آن بخش از تفتال که بر اثر کاهش فشار و فوران مقدار زیادی از گازهای محبوس در خود را از داده است گدازه نامیده می‌شود.

گدازه‌ها را بر پایه میزان سیلیس (Sio2) موجود در آنها از نظر میزان گرانروی به سه دسته بخش می‌کنند که این امر به دلیل اختلاف تعداد پیوند بین ملکولهای سیلیس است:

گدازه بازالتی: میزان سیلیس کم (حدود?? درصد). گرانروی کم، نقطه ذوب زیاد.
گدازه اندزیتی: میزان سیلیس متوسط (?? درصد). گرانروی متوسط. نقطه ذوب متوسط.
گدازه گرانیتی: میزان سیلیس زیاد ?? درصد). گرانروی زیاد. نقطه ذوب کم.

مهم‌ترین عوامل مؤثر در نوع آتشفشانها عبارت‌اند از ترکیب تفتال-دما و مقدار گازهای محلول در آنهاوفشار

رشته‌گدازه‌ای در هاوایی در سال 2003

گدازه ریسمانی^[?] (P?hoehoe) نوعی گدازه بازالتی است که سطحی نرم، موجدار و زبانه‌دار و ریسمانی دارد. این گونه گدازه هنگامی بوجود می آید که یک گدازه بسیار مایع‌گون بر روی یک سطح سفت‌شده جریان یابد.

فوران کمانی گدازه آتشفشانی در هاوایی

نظر شما ()

7:4 عصر شنبه 87/9/2

آتشفشان

نویسنده: امیررضا طغرلی

آتشفشان روزنه‌ای در سطح زمین است که سنگ‌های گداخته، خاکستر و گازهای درون زمین از آن به بیرون فوران می‌کنند.

فعالیت آتشفشانی با برون‌افکنی صخره‌ها، با گذشت زمان باعث پیدایش کوه‌های آتشفشانی بر سطح زمین می‌شود.

آتشفشان‌ها معمولاً در نقاطی یافت می‌شوند که ورقه‌های زمین‌ساخت، همگرایی یا واگرایی دارند.

آتشفشان:
?.حجره بزرگ تفتالی ?. سنگ‌بستر ?. مجرا ?. پایه ?. آذرین‌لایه ?. مجرای فرعی ?. لایه‌های خاکستر فوران‌شده ?. گُرده	?. لایه‌های گدازه ??. گلو ??. مخروط انگلی ??. جریان گدازه‌ای ??. دودکش ??. دهانه ??. ابر خاکستر

دید کلی می دانیم که زمین در ابتدا به حالت کره گداخته‌ای بوده است که پس از طی میلیونها سال بخش خارجی آن به صورت قشر سختی در آمد. این پوسته به دفعات بر اثر عبور مواد مذاب درونی سوراخ گردید و سنگهای آتشفشانی زیادی به سطح آن رسید. این عمل حتی در عصر کنونی نیز ادامه دارد. تمام پدیدههایی که با فوران تودههای مذاب بستگی دارند، پدیده آتشفشانی می‌گویند و علمی را که هدف آن بررسی این پدیده هاست با آتشفشان شناسی می‌نامند.

وقتی که از فعالیت آتشفشانی صحبت می‌شود در فکر خود فورانهای بزرگ ، سیلهایی از گدازه ، بهمن‌هایی از سنگهای گرم و خاکستر ، گازهای سمی و خطرناک و انفجارات شدید در نظر مجسم می‌نماییم که با مرگ و خرابی همراه است. به قول ریتمن کسی که این حوادث را می‌بیند هرگز نمی‌تواند فراموش کند و این امر به قدرت عظیم طبیعت و ضعف نیروی انسانی مربوط می‌باشد. بزرگترین آتشفشان کره زمین بزرگترین آتشفشان کره زمین مونالوآ نام دارد که بخشی از جزایر هاوایی را تشکیل می‌دهد. محیط قاعده مخروط این آتشفشان 600 کیلومتر و قله آن نسبت به کف اقیانوس که آن را احاطه کرده است 10 کیلومتر ارتفاع دارد. این آتشفشان ، همراه با سایر قسمتهای جزایر هاوایی نشاندهنده موادی هستند که به وسیله فورانهایی که از یک میلیون سال پیش تا کنون ادامه داشته‌اند، بیرون ریخته شده‌اند. بزرگترین آتشفشان کشف بشر بزرگترین آتشفشانی که تا کنون به وسیله بشر کشف شده است، الیمیوس مونز یا کوه المپیک نام دارد که در کره مریخ واقع است. شواهد به دست آمده از طریق عکسبرداریهای سفینه فضایی ماریند 9 نشان میدهد که ارتفاع این آتشفشان احتمالا 23 کیلومتر بوده و کالدرای آن نیز 65 کیلومتر عرض دارد. نمونه‌ای از فورانهای مهم دنیا آتشفشان وزوو آتشفشان مونالوآ آتشفشان پله آتشفشان بزیمیانی آتشفشان پاری کوتین در مکزیک آتشفشان نست هلن اقسام آتشفشانها آتشفشانهای نقطه‌ای که مواد گداخته از یک محل بیرون می‌آید (آتشفشان نوع مرکزی). انواع آتشفشانهای نقطهای عبارتند از:

آتشفشانهای نوع هاوایی یا سپری آتشفشانهای نوع استرومبولی آتشفشانهایی پرکابی آتشفشانهای نوع پله آتشفشانهای نوع ولکانو

آتشفشانهای شکافی یا خطی که فوران آن در امتداد یک شکاف صورت می‌گیرد. انواع آتشفشانهای شکافی یا خطی عبارتند از:

فورانهای خطی غیر انفجاری فورانهای خطی انفجاری

رابطه آتشفشان شناسی با سایر علوم زمینی ژئوفیزیک: برای اثبات و آگاهی از کانونهای درونی آتشفشانها و پیشگویی شکل و محل و موقعیت آن.

ژئوشیمی: تعیین دقیق عناصر که بصورت مواد جامد ، مایع و گاز از آتشفشان خارج می‌شوند.

ترمودینامیک: برای فهم و ارزیابی نیروی حرارتی آتشفشان و انرژی حاصله از آن و رابطه تشکیل مواد گداخته با حرارت و فشار و همچنین انجماد آن.

سنگ شناسی: جهت اطلاع از اختصاصات گدازه و شناسایی دقیق سنگهای آتشفشانی

رسوب شناسی: پراکندگی و نحوه انتشار مواد جامد آتشفشانی در دریاها و خشکیها که به صورت خاکستر ، توف ، برش و ... ته نشین می‌شوند. اهمیت آتشفشان شناسی از نظر اقتصادی: استفاده از انرژی گرمایی آن و انرژی گازهای فومرولی در گردش توربین و به دست آوردن مواد شیمیایی با ارزش که امروزه در ایتالیا ، زلاندنو ، ژاپن و ایسلند اهمیت پیدا کرده است و در کشور ما نیز اخیرا برای استفاده از نیروی حرارتی زمین (انرژی ژئوترمال) حفاریهایی انجام شده است.

پیشگیری از خطرات اجتماعی آتشفشان

اطلاع و آگاهی از ساختمان و ترکیب پوسته و تا اندازه‌ای گوشته زمین.

نظر شما ()

< 1 2 3 4 5 >> >

لیست کل یادداشت های این وبلاگ

مطالب طنز
[عناوین آرشیوشده]

[ خانه :: پارسی بلاگ :: مدیریت:: پست الکترونیک :: شناسنامه]

اوقات شرعی


	تعداد بازدید:66107
	امروز:34 دیروز :34 RSS


	درباره خودم
	امیررضا طغرلی


	لوگوی خودم



	لوگوی دوستان



	آرشیو
	تانژانت(ریاضیات) دایره مثلثاتی(ریاضیات) سینوس(ریاضیات) تابع(ریاضیات) گسل زمین شناسی گدازه آتشفشان باکتری ها جدول تناوبی عناصر1 جدول تناوبی عناصر2 عجایب هفت گانه احتمال گسسته(ریاضیات) هندسه ابوالحسن بنی صدر فرمول های مهم مثلثاتی(ریاضیات) قانون کسینوس ها(ریاضیات) فرمول اولر(ریاضیات) رادیان(ریاضیات) حل عددی معادلات دیفرانسیل معمولی(ریاضیات) جبر خطی(ریاضیات) فضای برداری(ریاضیات) دنباله(ریاضیات) تابع نمایی(ریاضیات) بهرام گور کروموزوم و میتوز عدسی ها(فیزیک) قانون کولن(فیزیک) ظرفیت گرمایی(فیزیک) قانون هوک(فیزیک) اخترشناسی1 اخترشناسی2 اخترشناسی3 اخترشناسی4 روباتیک باراک اوباما به روایت تصویر اسفند 1387


	اشتراک