|
||||||
|
به وبلاگ خودتون خوش آمدید |
||||||
|
|
به گسیختگی و یا شکست بخشی از پوسته زمین که به جابجایی چینههای آن میانجامد گُسَل یا گُسَله گفته میشود.
گسلهای بزرگ در پوسته زمین نتیجه حرکت برشی زمین هستند و زمینلرزهها نیز نتیجه نیروی رهاشده در حین لغزش سریع لبههای یک گسل به هم است. بزرگترین نمونههای گسل، مرزهای میان ورقههای زمینساختی کره زمین است. از آنجا که یک گسل معمولاً از یک شیار مستقیم و مرتب تشکیل نشده و ناحیهای از تغییر شکلهای پیچیده زمین را در بر میگیرد معمولاً بجای گسل از «منطقه گسلی» صحبت میکنند.
طبقه بندی زایشی گسل ها:
- گسل معکوس (RERVERSE) :
گسلی است که در آن کمر بالا(فرادیواره) به طرف بالا حرکت کرده باشد.
گسل معکوسیکه شیب آن کمتر از ?? درجه و بیشتر از ?? درجه باشد را گسل راندگی(THRUST) گویندو اگر شیب گسل کمتر از 10 درجه باشد ان را رورانده(OVER THRUST)مینامیم. توجه:گسل های رورانده ای که وسعت زیادی دارند را NAPPE (سفره)هم مینامند.
- گسل امتدادلغز (Strike Slip Fault یا Transcurrent Fault).
در این گسلها جابجایی کلی (لغزش کلی) در راستای امتداد گسل است، یعنی لغزش امتدادی بر لغزش شیبی برتری دارد. این نوع گسل دو حالت راستلغز(DEXTRAL) و چپلغز(SINISTRAL) دارد. گسل نرمال(NORMAL): در این نوع از گسل فرا دیواره به سمت پایین حرکت میکند توجه:گسل های نرمال کم شیب را گاهی اوقات LAG هم مینامند
طبقه بندی بر اساس شیب سطح گسل:
- گسلهای پرشیب (High angle faults)
- گسلهای کم شیب (Low angle faults)
- گسلهای قائم (Vertical faults)
- طبقهبندی براساس حالت گسل نسبت به چینهبندی
- گسل چینهای (Bedding Fault) (طبقهای)
- گسل مطابق و نامطابق
طبقهبندی براساس وضعیت گسل نسبت به طبقات اطراف
- گسل امتدادلغز (Strike Slip Fault)
- گسل موربلغز (Oblique Slip Fault)
- گسل طولی (Longitudinal Fault)
- گسل عرضی (Transvers Fault)
- گسل شیبلغز (Dip Slip Fault)
- گسل چرخشی (Pivotal Fault) یا محوری
طبقهبندی گسلها براساس طرح آنها
در این روش گسلها را بر مبنای وضعیت آنها نسبت به یکدیگر طبقهبندی میکنند. در این تقسیمبندی:
- گسلهای موازی (Parallel Fault)
- گسلهای محیطی (Peripheral Fault)
- گسلهای پَرمانند (Feather Fault)
- گسلهای پوششی (En Echelon Fault) (پلهای)
- گسلهای شعاعی (Radial Fault)
زمین شناسی یا ژئولوژی (Geology) از لغت یونانی Geo به معنی "زمین" و Logos به معنی "علم" یا "منطق" گرفته شده است. به عبارت دیگرزمین شناسی علم مطالعه زمین میباشد.
دید کلی:
زمین شناسی علمی است که درباره پیدایش زمین، تشکیلات ، ساختمان و مواد تشکیل دهنده زمین ، کوهها ، دشتها و اقیانوس و همچنین تاریخ پیدایش جانداران و تسلسل وقایع فیزیکی در زمین و بالاخره تحولاتی که در زمین صورت گرفته و میگیرد بحث مینماید. زمین شناسی در نیم قرن اخیر در جهان و در ربع قرن حاضر در ایران گسترش فراوانی یافت. بسیاری از نظریات سابق دگرگون شد و زمین شناس در بررسی سیاره پرارزش خود به آگاهیهای نوین دست یافت که پایه علوم زمین جدید را فراهم ساخت چون مانند همه رشتههای تجربی کار زمین شناسی بر اساس مشاهده و تغییر است لذا هر قدر امکان مشاهده مستقیم و غیر مستقیم ما ، از راههای ژئوفیزیک ، ژئوشیمی ، ماهوارهها و الکترونیک افزایش یابد، طبعا آگاهیهای ما هم از جهان و از گذشته کره زمین عمیقتر میگردد
· مدارک و اسناد حاکی از آن است که حدود 4500 سال قبل از میلاد ، انسان موفق به استخراج مس شد، حدود 2800 سال پیش از میلاد آلیاژ مفرغ بوسیله ایرانیان شناخته شد. در سالهای 1600 تا 1300 پیش از میلاد استفاده از آهن معمول گردید. قدیمیترین نقشه زمین شناسی در 2000 سال قبل از میلاد مربوط به معادن زمرد و طلا در مصر باقی مانده است.
· اینکه اولین مطالعات علمی زمین شناسی از چه زمانی آغاز شده به درستی مشخص نیست، شاید اولین نوشته در مورد این علم به وسیله ارسطو (332-348) سال قبل از میلاد) در کتاب "السما و العالم" به رشته تحریر در آمده باشد، که در آن از تغییرات وارد بر زمین و آثار جوی ذکر به میان آمده است. بعد از جنگ جهانی دوم (1945-1939) با پیشرفت علوم و تکنولوژی و در نتیجه احتیاج به مواد اولیه اهمیت علم زمین شناسی بیش از پیش آشکار شد. برای جستتجوی معادن فلزی و مخصوصا نفت ، زمین شناسان را بر آن داشت که دست به یک سری مطالعات جدید در زمینه ساختمانهای تحت الارضی زده و مطالب جدید کشف نمایند.
· در اوایل قرن بیستم با پیشنهادات وگنر ، نظر زمین شناسان به فرضیه اشتقاق قاره ها معطوف شد. در سالهای اخیر با مطالعات و توجهات بیشتر به نظریههای گسترش کف اقیانوس و تکتونیک صفحهای توسط دانشمندانی همچون مس و مورگان و با استفاده از پیشرفتهایی که در سایر علوم حاصل گردیده زمین شناسی وارد مرحله جدیدی از علوم شده است.
تعریف علم زمین شناسی:
· زمین شناسی دانش سیاره زمین است ودرباره منشا مواد و اشکال موجود بر آن صحبت میکند. گذشته این سیاره وفرایندهایی که برروی آن رخ داده یا درحال رخ دادن است و بر اشکال آن تاثیر دارد بررسی شود. برای حصول نتیجه از این مباحث در زمین شناسی باید اثر فشارهای مختلف مورد اثر بر زمین وهمچنین شیمی موادی که این سیاره از آن تشکیل شده واثر موجودات زمین در آن از جنبههای مختلف مورد بحث قرار گیرد. اطلاعات اولیه در مورد خود کره زمین نظیر پیدایش زمین عمر آن و وضعیت آن در فضا واز این قبیل ازطریق مطالعه سایر اجرام سماوی بدست میآید و گاها از این طریق با مطالعه وضع فعلی سایر اجرام شبیه زمین به طرز پیدایش رخدادها وتغییرات در گذشته زمین پی میبرند.
· تمام مطلعاتی که در مسیر شناخت زمین صورت میگیرد و علومی که در این مسیر پا گرفته و میگیرند در نهایت در خدمت جامعه بشری قرار میگیرد. در این علوم چگونگی استخراج واستفاده از مواد موجود در زمین و محیطهای زیستی پایدار در زمان پیدایش این مواد مورد بررسی قرار میگیرد و در علومی دیگر از خطرات ناشی از نیروهائی در حال حرکت و پویای موجود در زمین که ممکن است رفاه یا هستی انسانها را با خطر نیستی مواجه سازد آگاه میسازد. چون مواد موجود در زمین و ساختمانهای طبیعی موجود در آن از ابتدای تاریخ بشریت مورد استفاده انسانها بوده است میتوان گفت این علم از قدیمیترین علومی است که انسانها نا خودآگاه به آن پرداختهاند ودر طی قرون رفته رفته این علم و شاخههای متنوع آن مدون و طبقه بندی شدند و رشتههای فرعی وتخصصی با قوانین تعریف شده را به وجود آوردهاند که هریک بخشی از دانش زمین شناسی را تشکیل میدهند.
· زمین شناسی علمی است که به طور کلی در باره زمین صحبت میکند. این تعریف را باید کاملتر کرد. زیرا موضوع علوم دیگری نیز مثل هیات و نجوم و ... درباره زمین صحبت میکنند. ولی مقصود از زمین شناسی ، شناسایی و مطالعه تئوریهای پیدایش زمین و مواد تشکیل دهنده آن ، بررسی عواملی که در وضعیت آن تاثیر دارند. و بالاخره مطالعه و شناسائی مواد ارزشمند زمین و نحوه استفاده از آنهاست. زمین شناسی علم قدیمی و دارای سابقه طولانی است. و بشر همواره در مورد زمین کنجکاو بوده است. حوادثی مانند زلزله ، طوفان ، سیل ، گردباد و ... انسان را همواره در مورد زمین نگران می کرده. علم زمین شناسی ، یعنی آنچه که امروزه به علم جداگانه دارای رشتههای متنوعی است که بیش از دو سه قرن سابقه ندارد. و مانند سایر رشتههای علوم تحقیقات مداوم دانشمندان متعددی این علم را به پایه امروزی رسانده است.
نقش زمین شناسی در زندگی:
زمین شناسی علم قدیمی و سابقهداری است. اصولا بشر اولیه ، همیشه در مورد زمین کنجکاو بوده است. این کنجکاوی را میتوان معلول دو علت اساسی دانست. اول اینکه بشر و سایر موجودات زنده ، هستی خود را مرهون زمین بوده و همیشه غذای خود را از آن بدست میآوردهاند و بدین ترتیب مجبور بودهاند که دائما در مورد آن مطالعه کنند تا بتوانند غذای مناسب و حدالامکان متنوعی برای خود به دست آورند. نکته دومی که بشر را در مورد زمین نگران میکرده است، وقوع حوادث ناگواری مانند زلزله ، آتشفشان ، طوفان ، سیل و نظایر آن بوده که همیشه خسارات مالی و جانی زیادی را سبب میشده است و بشر به ناچار همواره در صدد بوده است که علل این حوادث را دریابد تا بتواند حتی المقدور از وقوع آن جلوگیری و یا حداقل آن را پیش بینی کند
تابع:
تابع را میتوان به عنوان هنجاری خاص برای تناظر بین اعضای دو مجموعه? دامنه و برد تعریف کرد. به بیان دقیقتر، اگر A و B دو مجموعه باشند، یک تابع از مجموعه? A به مجموعه? B را میتوان هنجاری تعریف کرد که به هر عضو مجموعه A چون a یک و فقط یک عضو از مجموعه B را چون (f(a نسبت میدهد. تابع f از مجموعه A به مجموعه B را با  نشان میدهیم.
نشان میدهیم.
برای نمونه تناظر شکل (?) نمایش دهنده یک تابع نمیباشد چراکه عضو ? به دو عضو متناظر شدهاست. اما شکل (?) نشان دهنده یک تابع است هر چند که دو عضو گوناگون به یک عضو نسبت داده شدهاند.
تابع f به عنوان هنجار تناظر، چیزی بجز توصیف نحوه تناظر اعضای A به B نیست که به طور کامل بهوسیله همه زوجهای مرتب ((a,f(a) برای هر a?A مشخص میشود پس تابع f را میتوان به عنوان مجموعه همه این زوجهای مرتب، یعنی مجموعه همه زوجهای مرتبی که مولفه اول آنها عضو A بوده و مولفه دوم آنها تصویر مولفه اول تحت تابع f است، تعریف کرد. شرط تابع بودن تضمین میکند که هیچ دو زوج متمایزی در تابع f دارای مولفه اول یکسان نخواهند بود.
در این صورت در تابع f:A?B برای هر a?A گزاره a,b)?f) را به صورت (b=f(a نشان میدهیم.
تعریف دقیق:
یک تابع از مجموعه X به مجموعه Y رابطهای چون f از مجموعه X به مجموعه Y است که دارای شرایط زیر باشد:
- دامنه f مجموعه X باشد، یعنی domf=X.
- برای هر x?X عنصر یگانه y?Y موجود باشد که x,y)?f) یا به عبارتی هیچ دو زوج مرتب متمایزی متعلق به f دارای مولفه اول یکسان نباشند. شرط یگانگی را به طور صریح میتوان یه این صورت فرمول بندی کرد که اگر x,y)?f) و x,z)?f) آنگاه y=z.
علامت ها:
برای هر x?X یگانه عضو y در Y که به ازای آن x,y)?f) را با (f(x نشان میدهیم. در مورد تابع این علامت گذاری، سایر علامت گذاریهایی را که در مورد روابط کلی تر استفاده میشوند چون x,y)?f) یا xfy را متروک ساختهاست. از این پس اگر f یک تابع باشد، بجای x,y)?f) یا xfy مینویسیم (y=f(x. عضو y را مقدار تابع به ازای متغیر یا شناسه x، یا تصویر x تحت f میگوییم و نیز x را پیش نگاره y میگوییم.
اگر f تابعی از مجموعه X به(در یا به توی) مجموعه Y باشد، این مطلب را به صورت سه تایی (f,X,Y) یا به طور معمول تر برای توابع با f:X?Y نشان میدهیم.
مسخص کردن تابع:
برای مشخص کردن یک تابع باید دامنه و ضابطه آن را بشناسیم. منظور از ضابطه یک تابع f:X?Y، فرمول و یا دستوری است که برطبق آن برای هر x?X، مقدار تابع f در x یعنی (f(x تعیین میشود. ضابطه تابع را میتوان به صورت یک گزاره جبری، مجموعهای از زوجهای مرتب یا یک رابطه بازگشتی مشخص کرد.
به این ترتیب برای مشخص کردن یک تابع از مجموعه X به مجموعه Y مینویسیم f:X?Y و سپس ضابطه آن را ذکر میکنیم.
در مواقعی که بیم ابهام نرود دامنه تابع ذکر نشده و به ذکر ضابطه تابع بسنده میشود. مثلاً عرف بر این است که در حساب دیفرانسیل و انتگرال دامنه توابع در صورت ذکر نشدن اعداد حقیقی یا بازهای از اعداد حقیقی باشد.
برای نمایش بهتر، تابع را که خود یک هنجار (قاعده) برای تناظر است با f نشان میدهیم و ورودی یا شناسه? این تابع را با x نشان میدهیم که ممکن است عدد هم نباشد. یگانه مقدار خروجی که هنجار f به ورودی x نسبت میدهد را بجای y اینبار با (f(x نشان میدهیم و آن را مقدار تابع f در x یا تصویر x تحت تابع f میگوییم. همچنین از این پس به هنجاری(قاعدهای) که هر x را به (y=f(x نسبت میدهد ضابطه تابع میگوییم.
نباید تابع را با ضابطه? آن اشتباه کرد. به عنوان مثال در مثال بالا f معرف خود تابع و گزاره (f(x معرف ضابطه تابع است.
دامنه و برد تابع:
یک تابع f از مجموعه X به توی مجموعه Y را به عنوان نوعی رابطه از مجموعه X به Y تعریف کردیم. مفاهیم دامنه (تابع) و برد همانگونه که برای روابط در حالت کلی قابل تعریفاند، به طریق اولی برای تابع f نیز قابل تعریف خواهند بود. بنا به تعریف دامنه تابع f که با domf نموده میشود، همان مجموعه X است. برد تابع f نیز مجموعه همه عناصری از Y است که تصویر عضوی از X تحت f باشند. برد تابع f را با ranf یا Imf نشان میدهیم. بنابه تعریف داریم:
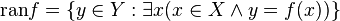
اما همانطور که در گذشته نیز اشاره شد و از تعریف فوق نیز قابل برداشت است، برد f در حالت کلی لزوماً برابر مجموعه Y نمیباشد بلکه زیرمجموعهای از آن است. برای تمایز بین مجموعه Y و برد تابع f به مجموعه Y همدامنه تابع f میگویند و آن را با codomf نشان میدهیم و بنا بر آنچه گفته شد، برد تابع زیرمجموعهای از همدامنهاش هست.
به عنوان مثال فرض کنید {X={????? و {Y={a,b,c,d و تابع f:X?Y به صورت {(f={(?,a),(?,b),(?,c تعریف شده باشد. وضوحاً دامنه این تابع مجموعه X است(میتوان برای تعیین آن مجموعه همه مولفههای اول زوجهای مرتب f را در نظر گرفت) ولی برد آن بنابه تعریف مجموعه {a,b,c} است که آشکارا زیرمجموعه حقیقی Y است.(یعنی زیرمجموعه آن است ولی با آن برابر نمیباشد)
در حقیقت برد تابع f مجموعه همه مولفههای دوم زوج مرتبهای f است. مجموعه همه عناصری از Y که به ازای یکx?X داشته باشیم (y=f(x.
تساوی دو تابع:
فرض کنید f:X?Y و g:Z?W دو تابع باشند. در این صورت تساوی f=g، تساوی بین دو مجموعه است و لذا f=g اگر و فقط اگر اعضای f و g یکسان باشند. یا به عبارتی دو تابع f و g با هم برابرند اگر و تنها اگر دامنهشان با هم برابر باشد و برای هر x از دامنه مشترکشان، (f(x)=g(x.
تجدید و توسیع:
فرض کنید f:X?Y یک تابع و A زیرمجموعهای از X باشد. در این صورت یک روش برای ساختن تابعی چون g از مجموعه A به مجموعه Y این است که برای هر g(x)، x?A را مساوی (f(x تعریف کنیم. یعنی تابع g:A?Y با ضابطه (g(x)=f(x. بر خوانندهاست که خوش تعریفی این تابع را تحقیق کند. ممکن است راه دیگری نیز برای بیان این مطلب بیابیم و آن این است که دامنه تابع f را به زیرمجموعه A از X تقلیل دهیم. در این صورت تابعی خواهیم داشت که این بار نه بر روی همه اعضای X بلکه فقط بر روی عناصر زیرمجموعه خاصی از X یعنی A اثر میکند و لذا دامنه آن از X به A تغییر مییابد. چنین تابعی را که همان g است تحدید تابع f به مجموعه A میگوییم و آن را با f|A یا f|A نشان میدهیم. با این نمادگذاری داریم g=f|A. همچنین تابع f را توسیع تابع g به مجموعه X میگوییم.
بنابراین مفاهیم تحدید و توسیع دو مفهوم متقابل به هم میباشند. تحدید یک تابع به زیرمجموعهای از دامنه خود همواره یک تابع است اما توسیع دامنه یک تابع به یک مجموعه جدید که دامنه تابع قبل زیرمجموعهای از آن است همواره تابع نمیباشد ولذا در مورد توسیع توابع احتیاط بیشتری لازم است. به طور کلی اگر f:A?Y یک تابع باشد توسیع تابع f به مجموعه X تابعی چون g با دامنه X است، به طوری که تحدید g به مجموعه A برابر تابع f باشد یعنی g|A=f.
هچنین میتوان همدامنه یک تابع را نیز تحدید کرد البته در این کار احتیاط لازم است، چراکه نباید اعضایی را که متعلق به برد تابع است را حذف نمود. اما اگر f:X?Y یک تابع باشد، با تحدید Y به (f(X که همان برد تابع f است میتوان تابع (f:X?f(X را تشکیل داد که پوشا نیز هست.
تصویر و تصویر معکوس:
اگر f:X?Y یک تابع و A زیرمجموعهای از X باشد، ممکن است بخواهیم مجوعهای را در نظر بگیریم که عناصر آن تصویر عناصر A تحت f میباشند. یعنی مجموعهای که از تأثیر تابع f روی هر عضو مجموعه A حاصل میشود. چنین مجموعهای را تصویر یا نگاره A تحت تابع f میگوییم و آن را با (f(A نشان میدهیم و به این صورت تعریف میکنیم:

بنابر این (y?f(A اگر وفقط اگر به ازای y= f(x)، x?A یا به بیان نمادین:
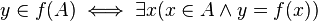
به عنوان مثال اگر {X={????????? و {Y={a,b,c,d,e و f:X?Y به صورت:
تعریف شود و زیرمجموعه A از X به صورت {A={????? در نظر گرفته شود در این صورت:
حال چون X نیز یک زیرمجموعهای از خودش است میتوان (f(X را نیز تشکیل داد، که در این صورت بنا به تعریف داریم:

که عبارت است از مجموعه همه عناصری از Y است که تصویر عضوی از X تحت f باشند که بنابه تعریف همان برد تابع f یعنی ranf است. به این ترتیب برد f را میتوان تصویر X تحت تابع f تعریف کرد.
اجتماع توابع-توابع چند ضابطه ای:
بسیار اتفاق میافتند که مقدار یک تابع در سراسر دامنهاش با یک ضابطه مشخص نمیشود مثلاً ممکن است دامنه تابع f که آن را X مینامیم را به n مجموعه X?,X?,X?,...,Xn افراز کنیم و تابع f با دامنه X را برای هر x?Xi به صورت (f(x)=fi(x تعریف کنیم که در آن fi تابعی با دامنه Xi است. همچنین در این صورت میتوان تابع f را برای هر x از دامنه به صورت زیر نوشت:
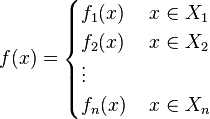
در این صورت f را تابعی با n ضابطه میگوییم.
در مثالی دیگر فرض کنید f:X?Y و g:Z?W دو تابع باشند که برای هر x متعلق به اشتراک X و Y (اشتراک دامنه f,g) داشته باشیم (f(x)=g(x. در این صورت تابع  اجتماع دو تابع f,g را به صورت زیر تعریف میکنیم:
اجتماع دو تابع f,g را به صورت زیر تعریف میکنیم:
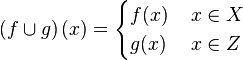
برخوانندهاست که خوش تعریفی این تابع را تحقیق کند. این مفهوم را میتوان گسترش داد یعنی اگر  خانوادهای از مجموعههای دو به دو جدا از هم باشد و برای هر fi,i?I تابعی با دامنه Ai باشد، میتوان تابع f، اجتماع توابع fi برای هر i?I را با دامنه
خانوادهای از مجموعههای دو به دو جدا از هم باشد و برای هر fi,i?I تابعی با دامنه Ai باشد، میتوان تابع f، اجتماع توابع fi برای هر i?I را با دامنه  را به صورت برای هر x از دامنه به صورت
را به صورت برای هر x از دامنه به صورت
(f(x)=fi(x اگر x?Ai تعریف کرد. در ادامه نمونههایی از توابع چند ضابطهای را خواهید دید.
نمودار تابع:
منظور از نمودار یک تابع f:X?Y به تصویر کشیدن تناظری است که f بین دو مجوعه X و Y ایجاد میکند. برای این کار برای همه روابط و بلاخص توابع عموماً از نمودار پیکانی استفاده میشود. برای رسم نمودار پیکانی تابع f:X?Y، دو منحنی بسته، نظیر آنچه در نمودار ون استفاده میشود را برای نمایش مجموعه X و Y انتخاب میکنیم و عناصر هر یک را بهوسیله نقاطی در آنها مشخص میکنیم. سپس بین هر عضو x?X و (f(x یک پیکان از x به (f(x به نشانه تناظر بین آن دو رسم میکنیم. به عنوان مثال اگر {X={????????? و {Y={a,b,c,d,e و f:X?Y به صورت {(f={(?,a),(?,b),(?,c),(?,d),(?,d تعریف شده باشد نمودار پیکانی آن به صورت مقابل است.
این روش گرچه مناسب است ولی برای نمایش همه توابع بویژه توابعی با دامنه اعداد حقیقی(و به طور کلی توابعی که عددی هستند) چندان کاربرد ندارد. اگر f تابعی با دامنه اعداد حقیقی R باشد آن را تابع حقیقی میگوییم و برای نمایش نمودار آن از دستگاه مختصات دکارتی استفاده میکنیم و روش کار به این صورت است که برای هر x?R زوج مرتب ((x,f(x) که نماینده نقطهای در صفحه دکارتی است را رسم میکنیم و به این ترتیب نمودار تابع f حاصل میشود. رسم نمودار تابع، باعث میشود دیدی کلی نسبت به آن تابع پیدا کنیم و همچنین بسیاری از خواص مربوط به توابع بویژه توابع حقیقی مانند پیوستگی، مشتق پذیری، نقاط بحرانی و عطف، صعودی یا نزولی بودن و... از روی نمودار آنها قابل تعیین است. به عنوان مثال با بررسی شکل (?) میتوان گفت این تابع در چه بازههایی صعودی و در چه بازههایی نزولی است، این تابع در سراسر دامنه خود پیوسته و مشتق پذیر است، دارای دو نقطه بحرانی و یک نقطه عطف است و....
همچنین از روی نمودار یک رابطه میتوان تابع بودن آن را بررسی کرد. به عنوان مثال نمودار شکل (?) معرف یک تابع نیست، زیرا عضو ? به دو مقدار متناظر شدهاست. همچنین در نمودار رسم شده در دستگاه دکارتی در شکل (?)، برای هر عدد حقیقی مثبت x دو مقدار وجود دارد. به طور کلی یک نمودار در دستگاه مختصات دکارتی یک تابع است اگر هر خط عمودی مرسوم بر محور xها نمودار را حداکثر در یک نقطه قطع کند.
فضای توابع:
اگر X و Y دو مجوعه باشند مجموعه همه توابع از مجموعه X به مجموعه Y را با YX نشان میدهیم و بنابه تعریف داریم:
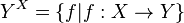
عدد اصلی این مجموعه را نیز میتوان به صورت زیر بدست آورد(برای اثبات به مقاله حساب اعداد اصلی رجوع کنید.):
از رابطه فوق نتیجه میشود اگر X مجوعهای n عضوی و Y مجموعهای m عضوی باشد تعداد توابع قابل تعریف از مجوعه X به مجموعه Y برابر است با mn که البته برای اثبات این مسئله خاص راه حل ترکیباتی هم وجود دارد. توضیح اینکه اگر بخواهیم تابع f:X?Y را تعریف کنیم هر عضو از n عضو مجموعه X چون x?X، را میتوان به m طریق به یک عضو از مجموعه Y نسبت داد. پس بنا بر اصل شمارش تعریف چنین تابعی به mn طریق ممکن خواهد بود.
توابع دو یا چند متغیره:
عباراتی چون f(x,y) = sin(xy) یا f(x,y,z) = x2 + y2 + z2 را در نظر بگیرید. هر یک از آنها دو یا بیش از دو متغیر از دامنه میپذیرند و یک مقدار یگانه را به آنها نسبت میدهند. گاهی ممکن است تابع بجای یک شناسه دو یا چند شناسه را به بپذیرد و آنها را به یک عضو از برد خود نسبت دهد، در این صورت تابع را دو یا چند متغیره میگوییم. چنین توابعی رابطهای بین بیش از دو مجموعه هستند. به عنوان مثال تابع اول را میتوان تابعی به صورت f:R×R?R توصیف کرد که در این صورت تابع زوج (x,y) را به عنوان شناسه خود میپذیرد و آن را به عضوی از R نسبت میدهد که در این صورت اعضای تابع f را میتوان به صورت سه تایی ((x,y,f(x,y) نشان داد.
پیشینه:
تابع به عنوان مفهومی در ریاضیات، توسط گاتفرید لایبنیز در سال ????، با هدف توصیف یک کمیت در رابطه با یک منحنی مانند شیب یک نمودار در یک نقطه خاص به وجود آمد. امروزه به توابعی که توسط لایبنیز تعریف شدند، توابع مشتقپذیر میگوییم.
واژه تابع بعدها توسط لئونارد اویلر در قرن هجدهم، برای توصیف یک گزاره یا فرمول شامل متغیرهای گوناگون مورد استفاده قرار گرفت، مانند f(x) = sin(x) + x?.
در طی قرن نوزدهم، ریاضیدانان شروع به فرمول بندی تمام شاخههای ریاضی براساس نظریه مجموعهها کردند. وایراشتراس بیشتر خواهان به وجود آمدن حساب دیفرانسیل و انتگرال در علم حساب بود تا در هندسه، یعنی بیشتر طرفدار تعریف اویلر بود.
در ابتدا، ایده تابع ترجیحاً محدود شد. ژوزف فوریه مدعی بود که تمام توابع از سری فوریه پیروی میکنند در حالی که امروزه با گسترش تعریف توابع، ریاضیدانان توانستند به مطالعه توابعی در ریاضی بپردازند که که در سراسر دامنه خود پیوسته ولی در هیچ نقطهای مشتقپذیر نیستند این گونه توابع توسط وایراشتراس معرفی شدند. کشف چنین توابعی موجب شد تا توابع تنها به توابع پیوسته و مشتقپذیر محدود نشوند.
تا انتهای قرن نوزدهم ریاضیدانان در هر موضوع ریاضی به دنبال تعریفی بودند که براساس نظریه مجموعهها و نتایج آن باشد. دیریکله و لوباچوسکی هر یک به طور مستقل همزمان تعریف «رسمی» از تابع ارائه دادند.
بر طبق این تعریف، تابع حالت خاصی از یک رابطه است که در آن برای هر مقدار اولیه یک مقدار ثانویه منحصر به فرد وجود دارد.
تعریف تابع در علم رایانه، به عنوان حالت خاصی از یک رابطه، به طور گستردهتر در منطق و علم تئوری رایانه مطالعه میشود.
در سایر علوم:
توابع در شاخههای مختلف علوم کاربرد فراوان دارند. برای مثال در فیزیک، هنگامی که میخواهیم رابطه بین چند متغیر را بیان کنیم، مخصوصاً هنگامی که مقدار یک متغیر کاملاً وابسته به متغیرهای دیگر است از توابع استفاده میشود.
توابع در علوم مختلف بیشتر به عنوان عملگر در نظر گرفته میشوند که کاری را بر روی ورودیهای خود انجام میدهند. توابع را همچنین مورد استفاده در علم رایانه برای مدلسازی ساختمان دادهها و تأثیرات الگوریتم میبینیم.
سینوس، از تابعهای مثلثاتی است که عددی را به هر زاویه نسبت میدهد. این عدد برابر است با نسبت طول ضلع مقابل زاویه به طول وتر در مثلث راستگوشه فرضی که با زاویه مورد نظر ساخته شده باشد.
سینوس را در متنهای عربی و فارسی قدیم «جیب» مینامیدند.
اگر با زاویه A مثلث راستگوشه ABC را بسازیم، سینوس این زاویه برابر است با نسبت طول ضلع مقابل به طول وتر، یعنی sin(A) = a / h
تانژانت، یکی از نسبتهای مثلثاتی که در ریاضیات و اخترشناسی کاربرد فراوان دارد و در گذشته به آن ظل میگفتند.
این نسبت مثلثاتی چنین تعریف میشود: نسبت ضلع مقابل به زاویه مورد نظر، به ضلع مجاور آن در مثلث قائمالزاویه.
در نمودارهای دو بعدی که معادله یک خط را نشان میدهند شیب نمودار (یا خط مماس بر نمودار) برابر است با تانژانت زاویهای که خط با جهت مثبت محور افقی (محور xها) میسازد.
تاریخچه:
ظل (از عربی، به معنای سایه) اصطلاحی است که در گذشته در متنهای اسلامی و ایرانی برای تانژانت در ریاضیات و اخترشناسی بهکار میرفت.
ستارهشناسی به نام حبشبن حاسب اولین بار در قرن سوم هجری قمری (قرن نهم میلادی) این نسبت مثلثاتی را به کار برد[?].
سید اَبوالحسن بَنیصدر زاده? 2 فروردین 1312(22 مارس 1933) اقتصاددان و سیاستمدار ایرانی است. او در بهمن سال 1358 به عنوان نخستین رئیس جمهور ایران، انتخاب شد و در خرداد 1360، به دلیل «عدم کفایت سیاسی»، توسط مجلس شورای اسلامی از مقام خویش عزل گردید.
پیش از انقلاب ??
بنیصدر در باغچه از توابع همدان بدنیا آمد.[?] پدرش آیت الله سیدنصرالله بنی صدر، از روحانیون با نفوذ همدان [?] بود که با آیت الله روحالله خمینی نیز ارتباط دوستانهای داشت. او در دانشگاه تهران، در رشته های اقتصاد و حقوق اسلامی تحصیل کرد و چهار سال در موسسه مطالعات و تحقیقات اجتماعی فعالیت نمود. بنیصدر رهبری گروه کوچکی از دانشجویان مخالف رژیم شاه را بهعهده داشت و دوبار به خاطر فعالیتهای سیاسی دستگیر و روانه زندان شد. پس از مجروح شدن در قیامی ناموفق علیه حکومت در خرداد 1342، او کشور را ترک و عازم فرانسه شد.[?] بنیصدر به همراه حسن حبیبی (معاون اول اسبق برخی از روسای جمهور ایران) جزء دانشجویانی بود که به همت احسان نراقی، نظریه پرداز و محقق وابسته به فرح دیبا برای ادامه تحصیل به اروپا رفت. این دو نفر از شاگردان نراقی نیز بودهاند.[?][منابع بیشتری نیازست] او در دانشگاه سوربون پاریس دکترای خویش را احراز نمود و به تدریس در دانشگاه پرداخت.[?]
بنی صدر در دهه هفتاد میلادی و سالهای پیش از پیروزی انقلاب، به عنوان یک ناسیونالیست اسلامی پرشور و اقتصاددان انقلابی با ایراد سخنرانی و چاپ و انتشار مقالات و کتب تالیفی خود، به مبارزه با حکومت شاه میپرداخت.[?] به عقیده هاشمی رفسنجانی، در طی این سالها بنیصدر که نزدیکی بیشتری با جبهه ملی احساس میکرد و خود را تئوریسین انقلاب میدانست همواره درگیر رقابت با صادق قطب زاده (که او نیز در پاریس اقامت داشت) بود. قطب زاده نزدیکی فکری بیشتری با نهضت آزادی داشت و به همین لحاظ بیشتر مورد تائید مبارزین اسلامی بود.[?]در سال ?? و اندکی پیش از پیروزی انقلاب، با ورود آیت الله خمینی به پاریس، او جزء معدود کسانی بود که در فرودگاه به استقبال او آمد[?] و سپس به جمع همراهان او پیوست. پس از ناآرامیها و آشوبهای داخلی که سبب فرار شاه از ایران شد، این دو در تاریخ 12 بهمن سال 1357با پرواز ایرفرانس (که بنی صدر کرایه چارتر آنرا با چک بلامحل خودش پرداخته بود[?]) به کشور بازگشتند.
ابتدای پیروزی انقلاب
بعد از پیروزی انقلاب 1357 خمینی که عهده دار کنترل کشور بود، پس از به کار گماردن دولت موقت، بنی صدر را ابتدا در ماه تیر 58 به معاونت وزارت اقتصاد و دارایی و سپس درماه آبان به سمت وزیر منصوب کرد.[?] بنی صدر همچنین مدتی به عضویت شورای انقلاب در آمد و سپس با بروز بحران گروگانگیری کارکنان سفارت آمریکا در تهران، به یکی از تصمیم گیرندگان و مخالفین اصلی آن تبدیل شد. رقابت وی با قطب زاده، باعث شد حل این بحران 444 روز به طول بیانجامد.[?][??] مدتی بعد از استعفای دولت موقت مهندس مهدی بازرگان، او با حمایت جامعه روحانیت مبارز[??] برای انتخابات ریاست جمهوری کاندید شد و در پنجم بهمن ماه 1358 با به دست آوردن یازده میلیون رای به عنوان اولین رئیس جمهور تاریخ ایران انتخاب گشت. او دراین انتخابات، 76 درصد آرا را کسب کرد. رقبای وی در این انتخابات آقایان (حسن حبیبی، احمد مدنی، صادق طباطبایی، داریوش فروهر، صادق قطبزاده، کاظم سامی، محمد مکری، حسن غفوریفرد و حسن آیت[??]) بودند و تعداد آرای این افراد مجموعا بیست و سه درصد آرای باقیمانده را تشکیل میداد.
پس از ریاست جمهوری
یک ماه پس از پیروزی بنیصدر در انتخابات، او از سوی آیتالله خمینی به ریاست شورای انقلاب که هیات سیاستگذار و نظریه پرداز ایران محسوب میشد، منصوب گشت. خمینی همچنین به منظور تقویت موقعیت او، سمت فرماندهی کل قوا را نیز به او محول کرد.[??] . او از روی اکراه و تحت فشارها، محمد علی رجایی را که مورد تایید او نبود در مرداد 1359 به سمت نخست وزیری دولت خویش انتخاب کرد و مدت کوتاهی پس از عدم قبول بنی صدر در پذیرفتن نامزدهای منتخب رجایی برای کابینه دولت، روابط ایندو به تیرگی و ناسازگاری گرایید. مدتی بعد در ماه مهر همان سال عراق به خاک ایران یورش برد که آتش جنگی هشت ساله بین این دو کشور را برافروخت.[?] به جز اختلاف نظر و درگیری او با نخست وزیر و اعضای کابینه، او در ابتدای جنگ به سیاستهایی معتقد بود که موجب مخالفت حزب جمهوری اسلامی و مجلس و روحانیونی که پیشتر از او حمایت کرده بودند، شد. حزب، روزنامه جمهوری اسلامی را منتشر میکرد و بنی صدر شروع به انتشار روزنامه انقلاب اسلامی (که از تیراژ بیشتری برخوردار بود) نمود.
در نهم ماه آبان، بنیصدر طی نامهای رسمی به خمینی، اعتراض خود را مبنی بر اینکه وزیران بی کفایت تهدیدی بزرگتر از تجاوز عراق به خاک کشور برای امنیت محسوب میشوند، نشان داد. وی همچنین در این نامه عنوان کرد که هشدارهایش درمورد وخیمتر شدن اوضاع اقتصادی و پافشاریهایش مبنی بر نیاز به سازماندهی مجدد نیروهای مسلح، نادیده انگاشته شدهاند. این نامه و همچنین مخالفتهای او در گروگان گیری اعضای سفارت آمریکا در تهران، خشم مجلس وقت (که اکثریت آن از اعضای حزب جمهوری اسلامی تشکیل میشد) را بر انگیخت[?] و در تاریخ 31/3/1360 مجلس شورای اسلامی با اکثریت177نفر در مقابل 12 رای ممتنع و یک رای مخالف رأی بر عدم کفایت او داد.[??] حکم مجلس یک روز بعد به امضای خمینی رسید که پیش از آن نیز از مذاکرات بنیصدر با سازمان مجاهدین خلق که یک گروه ضد حکومت وقت محسوب میشد، ناراضی بود.
بنی صدر شش هفته بعد به همراه مسعود رجوی (رئیس سازمان مجاهدین خلق) با تغییر چهره و لباس از فرودگاه مهرآباد و با هواپیمایی که بهزاد معزی هدایت آن را برعهده داشت از ایران گریخت و وارد فرودگاه پاریس شد. خروج بنیصدر و رجوی از کشور به این روش مخاطرهآمیز و غیرعادی توجه رسانهها را به خود جلب کرد.[نیازمند منبع]
در فرانسه بنیصدر، رجوی را در تاسیس شورای ملی مقاومت، گروهی که وقف براندازی حکومت خمینی شده بود، یاری کرد. در سال 1984 میلادی، وی به خاطر اختلاف نظر با رجوی، از شورا خارج شد.[?] او همچنین در این دوران با فرح دیبا (همسر شاه سابق) ملاقاتهایی در قاهره داشت.[??]
سایر رئیس جمهورها در روزهای آتی
< type=text/java>
// if (window.showTocToggle) { var tocShowText = "نمایش"; var tocHideText = "نهفتن"; showTocToggle(); }
//]]>

همانطور که می دانید ارسطو در قرن چهارم نظریه تحت عنوان نظریه خلق الساعه داده بودکه تاقبل از آن که لویی پاستور با آزمایشی کاملا کنترل شده بتواند آن تکدیب کند بر این نظریه معتفد بودند .
طبق این نظریه مگس از مواد گندیده به وجود می آمد یا مارمولک از خشت به وجود می آید.سپس لویی پاستور با آزمایش خود آن زا به طور کامل تکذیب کرد که آزمایش این گونه بود :
محلول غذایی را تهیه کرد ( آبگوشت ) سپس درون شیشه ای با کمر باریک وبلند ریخت سپس با حرارت گردن آن را به شکل S در آورد تا چیزی نتواند وارد آن شود سپس محلول را چند دقیقه در حرارت بسیارزیاد جوشاند تا حتی میکروب های درون آن هم از بین برود و عاری از هر گونه مواد آلی شود سپس محلول را در فضای آزاد گذاشت تا سرد شود
نتیجه : فقط در صورتی از مواد آلی چانداری به وجود می آید که سلول های زنده ای از قبل در آن باشد به عبارت دیگر در صورتی چانداری در چایی به وجود می آید که از قبل در آنجا موجودی وجود داشته باشد
از عجایب هفت گانه چه می دانید؟
این هفت بنای باستانی از آن جهت برای مردم بسیار عجیب به نظر می رسند که انسانهای قدیم آنهارا با کمک ابزارهای بسیار ابتدایی بنا نهاده اند وکاری ما فوق دانش روزگار خود انجام داده اند.
اهرام مصر
ساختن اهرام در سرزمین مصر به فرمان فرعونها از سه هزار سال قبل ازمیلاد مسیح آغاز شد (حدود ???? سال قبل) وآخرین آنها در سال ???? قبل ازمیلاد به پایان رسید هر فرعون برای خود هرمی می ساخت تا آرامگاه ابدی او باشد تا به اعتقاد مصریان زمانی که روح به بدن پادشاه برمیگردد بتواند در بدن اوکه مومیایی می شد جای بگیرد وفرعون د وباره بتواند زندگی را ازسر بگیرد وبه همین علت معمولا بدن مومیایی شده فرعون را تابوتی که به شکل صورت او ساخته شده بود قرار می داد ند ودر کنارش مجموعه ای ازلوازم زند گی - خوراک - پوشاک و حتی کشتی اختصاصی اش را دفن می کردند هر هرم طی دهها سال و توسط صد ها هزار برده ساخته می شد. قدیمی ترین هرم مصر در ناحیه ساکارا قرار دارد وبزرگترین و کامل تر ین هرم که جزو عجایب هفتگانه به شمار می رود هرم خئوپس است که که در نزدیکی جیزه قرار دارد این هرم در حد ود ?? جریب زمین مساحت دارد و ارتفاع اصلی آن ??? متر بوده که به مرور زمان به ??? متر کاهش پید ا کرده است.
باغهای معلق بابل
گفنه می شود که این باغها توسط بخت النصر ساخته شد وی بعد از ویران کردن معبد سلیمان در محل بیت المقدس کنونی در سال ??? قبل از میلاد این باغهای معاق را برای ملکه خو د که د ختر هوخشتر پادشاه قدرتمند ماد بود بنا کر د این باغ 5 طبقه داشت هر طبقه با ?? متر فاصله بر روی طبقه زیرین ساخته شده بود و در هر طبقه گلها وگیاهان فراوانی را کاشته بودند وشاید از آن جایی که شاخ وبرگ درختان به سمت طبقه های زیرین آویزان می شده آن را باغهای معلق گفته اند البته باید اضافه کرد کشور بابل در منطقه عراق کنونی واقع بود.
مجسمه زئوس
مجسمه زئوس در سال ??? قبل از میلا د در شهر المپیا ساخته شد شهری که بازیهای المپیک از آنجا آغاز شد این مجسمه که شاهکاری از هنر و دانش بشری بود به نشانه احترام وپرستش زئوس که به اعتقاد یونانیان خدای خدایان بود بر پا شده بود جنس مجسمه از سنگ مرمر خالص بود وبرای تزئئن بخش های گوناگون آن از طلا وعاج استفاده کرده بودند و بلندای آ ن به ?? متر می رسید این شاهکار هنری بر اثر جنگهای گوناگون به کلی از بین رفت.
معبد دیانا
این معبد ??? قبل از میلا د مسیح در ناحیه افه سوس در ترکیه کنونی ساخته شد ساخت این معبد آنقد ر مهم بود که مردم شهرهای گوناگون با فرستادن هدایایی در ساحت آ ن شرکت کرد ند و پس از تکمیل از تمامی نقاط برای زیارت آن می آمد ند طول و عرض معبد ??? در ?? متر بود و ?? ستون از مرمر خالص سقف آن را نگه می داشت که هر کدام از این ستون ها حدود ?? متر ارتفاع داشتند ولی در سال ??? بعد از میلاد اروس توستن فقط به خاطر کسب شهرت وقد رت این بنا را به آتش کشید اما بعد مدتی آنرا تعمیر کردند و تالار جدیدی برای آن ساختند وسرانجام به فرمان نرون آن جا را به کلی ویران ساختند.
مجسمه آپولو
گفته می شود که مجسمه آپولوکه یکی از خدایان یونان قدیم بوده است درنزد یکی آسیای صغیر و در مدخل خلیج رودس برپا شده بود این مجسمه از جنس برنز و به ارتفاع ?? متر ساخته شده بود نصب این مجسمه بر روی زمین از شاهکارهای معماری محسوب می شده و مخصوصا حالت ایستاده آپولو در حالی که پاهای خودرا باز کرده بسیار جالب بوده است اما مجسمه در سال ??? قبل از میلاد مسیح بر اثر یک زلزله شدید سرنگون شد و تا سالیان درازی به همان ترتیب بر روی زمین باقی ماند پس از مدتی مردم برای استفاده از فلز برنز بدن مجسمه تکه های آن را جدا کردند تا آنکه بالاخره چیزی از آن باقی نماند.
آرامگاه ماسولوس
در سال ??? قبل از میلاد هنگامیکه ماسولوس پادشاه کاریس در ترکیه کنونی درگذ شت آرامگاه باشکوهی از مرمر خالص برای اودر شهر هالیکارناس بنا کرد ند این ساختمان چهار گوش و محیط آن ??? متر بود و سقفی هرمی شکل داشت که بر روی تعدادی ستون استوار بود و بر بالای آن مجسمه کالسکه پیروزی با چهار اسب که شاه وملکه بر آن سوار بودند نصب دیده می شد بلندی این مقبره به بیش ار ?? متر می رسید و بارها توسط اعراب و بربر ها مورد حمله قرار گرفت تا اینکه به سبب زلزله شدیدی از بین رفت اما در قرن نوزده میلادی بخشهایی از کشف گردید که هم اکنون در موزه بریتانیا نگهداری می شود.
فانوس دریای اسکندریه
شاید قابل استفاده ترین این بناهای هفتگانه چراغ دریایی بود که در بندر اسکندریه مصر برپا شده بود این بنا ??? پیش از میلاد مسیح توسط یکی از فراعنه وبرای تقدیم به یکی از خدایان برپا شده بود این ساختمان که بر بالای آن کوهی از آتش برپا می شد وظیفه راهنمایی کشتی ها را داشت و در حقیقت اولین چراغ دریایی جهان بوده است این فانوس دریایی تا ??? سال به خوبی انجام وظیفه کرد تا آنگه سر انجام بر اثر زلزله ای کاملا از بین رفت.
در ریاضیات دایره مثلثاتی دایرهای به شعاع واحد است. x و y دو مختصه روی این دایره هستند که بنا به تعریف دایره: x2 + y2 = 1.
نقطه (x, y) روی این دایره با (?, ?) زاویهای میسازد که از روابط زیر بدست میآید:


بنابر این خواهیم داشت:
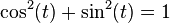
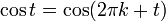

که در آن k عددی صحیح است. سایر توابع مثلثاتی نظیر تانژانت و کتانژانت و سکانت و کسکانت را میتوان به همین ترتیب بدست آورد.
لیست کل یادداشت های این وبلاگ
[ خانه :: پارسی بلاگ :: مدیریت:: پست الکترونیک :: شناسنامه]